Question

Find the 270 degrees value for all the trigonometric angles.

Answer 1

Hint:We explain the process of finding values for associated angles. We find the rotation and the position of the angle of ${{270}^{\circ }}$ for all trigonometric ratios. We explain the changes that are required for that angle. Depending on those things we find the solutions.

Complete step by step answer:
We need to find the ratio value of ${{270}^{\circ }}$ for all trigonometric ratios. For general form, we need to convert the value of x into the closest multiple of $\dfrac{\pi }{2}$ and add or subtract a certain value $\alpha $ from that multiple of $\dfrac{\pi }{2}$ to make it equal to $x$. Let’s assume $x=k\times \dfrac{\pi }{2}+\alpha $, $k\in \mathbb{Z}$. Here we took the addition of $\alpha $. We also need to remember that $\left| \alpha \right|\le \dfrac{\pi }{2}$. Now we take the value of $k$. If it’s even then keep the ratio as it is and if it’s odd then the ratio changes to its corresponding related ratios.

The connected ratios are sin with cos, tan with cot, sec with cosec. Then we find the position of the given angle as a quadrant value measured in counter clockwise movement from the origin and the positive side of the X-axis.The sign of the trigonometric ratio is positive for the excess angle in their respective quadrants according to the below image.

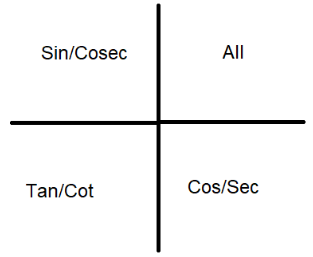
Depending on the sign and ratio change the final angle becomes $\alpha $ from x.
Now we find the final values of ${{270}^{\circ }}$ for all trigonometric ratios.
$\sin 270=\sin \left( 3\times \dfrac{\pi }{2}+0 \right)=-\cos \left( 0 \right)=-1$
$\Rightarrow \cos 270=\cos \left( 3\times \dfrac{\pi }{2}+0 \right)=\sin \left( 0 \right)=0$
$\Rightarrow \cot 270=\cot \left( 3\times \dfrac{\pi }{2}+0 \right)=-\tan \left( 0 \right)=0$
$\Rightarrow \csc 270=\dfrac{1}{\sin 270}=-1$
$\Rightarrow \sec 270=\dfrac{1}{\cos 270}=\dfrac{1}{0}=\text{undefined}$
$\Rightarrow \tan 270=\dfrac{1}{\cot 270}=\dfrac{1}{0}=\text{undefined}$

Note:We need to remember that the easiest way to avoid the change of ratio thing is to form the multiple of $\pi $ instead of $\dfrac{\pi }{2}$. It makes the multiplied number always even. In that case we don’t have to change the ratio. If $x=k\times \pi +\alpha =2k\times \dfrac{\pi }{2}+\alpha $. Value of $2k$ is always even.