Question

Find out the centre of mass of an isosceles triangle of base length a and altitude b. Assume that the mass of the triangle is uniformly distributed over its area.
A. $\dfrac{{2b}}{3}$ from the base
B. $\dfrac{{2b}}{3}$from the vertex
C. $\dfrac{b}{4}$ from the base
D. $\dfrac{{3b}}{4}$ from the vertex

Answer 1

Hint: In such types of questions of variable or uniform distribution of mass we use the method integration. Doing this will solve your problem and will give you the right answer.

Formula used: \[{x_{CM}} = \dfrac{1}{M}\smallint xdm\]

Complete step-by-step solution -

The moment of inertia is defined as the ratio of the net angular momentum of the system to its angular velocity around the main axis, that is. Unless the angular momentum of the system is unchanged, the angular velocity will increase as the moment of inertia decreases.
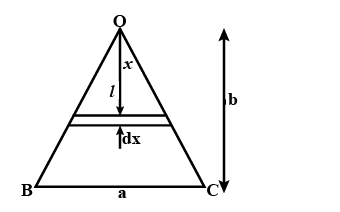
Given, base length =a
Altitude = b
To locate the center of mass of the triangle, we take a strip of width dx at a distance x from the vertex of the triangle. Length of this strip can be evaluated by similar triangles as
\[I = x.(\dfrac{a}{b})\]
Mass of the strip is \[dm = \dfrac{{2M}}{{ab}}ldx\]
Distance of center of mass from the vertex of the triangle is
\[{x_{CM}} = \dfrac{1}{M}\smallint xdm\]

$ = \int_0^b {\dfrac{{2{x^2}}}{{{b^2}}}dx} \\
   = \dfrac{2}{3}b \\ $

Hence, the correct answer is \[\dfrac{2}{3}b\] and the correct option is (B).

Note: The center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. Centre of mass of a figure in X- coordinate and Y- coordinate is \[{y_{CM}} = \dfrac{1}{M}\smallint ydm\] \[{x_{CM}} = \dfrac{1}{M}\smallint xdm\] and \[{y_{CM}} = \dfrac{1}{M}\smallint ydm\] respectively.