Question

How do you find its vertex, axis of symmetry, y-intercept and x-intercept for $f(x)=-3{{x}^{2}}+3x-2$?

Answer 1

Hint: We are given with a quadratic equation using which the above mentioned properties have to be found. Since the equation is of the form \[y=-{{x}^{2}}\], so it is a parabola open towards the negative y – axis. And we will find the axis of symmetry and x-vertex using the formula \[x=\dfrac{-b}{2a}\] and for y –vertex, substitute the value x – vertex in the given equation. Y-intercept is found by keeping \[x=0\] and vice – versa.

Complete step by step solution:
According to the given question, we have been given a quadratic equation, whose mentioned properties we have to find.
We have the given expression as
$f(x)=-3{{x}^{2}}+3x-2$----(1)
Here, \[a=-3,b=3,c=-2\]
We will begin with vertex.
Vertex of a parabola can simply be said as the intersection point between the line of symmetry and the parabola.
X – coordinate of vertex \[=\dfrac{-b}{2a}\]
On substituting, we get it as,
\[\Rightarrow \dfrac{-3}{2(-3)}\]
\[\Rightarrow \dfrac{1}{2}\]
So, we have the x-coordinate of the vertex. For y- coordinate, we will substitute the value of x in the equation (1), we get,
\[y=-3{{x}^{2}}+3x-2\]
\[\Rightarrow y=-3{{\left( \dfrac{1}{2} \right)}^{2}}+3\left( \dfrac{1}{2} \right)-2\]
\[\Rightarrow y=-3\left( \dfrac{1}{4} \right)+3\left( \dfrac{1}{2} \right)-2\]
\[\Rightarrow y=\dfrac{-3}{4}+\dfrac{3}{2}-2\]
\[LCM(4,2)=4\]
\[\Rightarrow y=\dfrac{-3}{4}+\dfrac{3}{2}\times \dfrac{2}{2}-2\times \dfrac{4}{4}\]
On solving further, we get,
\[\Rightarrow y=\dfrac{-3}{4}+\dfrac{6}{4}-\dfrac{8}{4}\]
\[\Rightarrow y=\dfrac{-3+6-8}{4}\]
\[\Rightarrow y=\dfrac{-5}{4}\]
So, the vertex of the parabola is \[\left( \dfrac{1}{2},\dfrac{-5}{4} \right)\].
As we have stated that vertex is the intersection of the line of symmetry and the parabola. And the equation of parabola we have is open towards the negative y-axis. This means that the x – coordinate of the vertex is the same as the equation of line of symmetry passing through the vertex.
Therefore, the line of symmetry is \[x=\dfrac{1}{2}\].
Now, we will find the y – intercept. We know that, y- intercept refers to the point when the given equation intersects with y- axis, so at that point we have \[x=0\]. Therefore, to find the y-intercept we will put \[x=0\] in the given quadratic equation.
We have,
\[y=-3{{x}^{2}}+3x-2\]
Substituting \[x=0\], we get,
\[\Rightarrow y=-3{{(0)}^{2}}+3(0)-2\]
\[\Rightarrow y=-2\]
Therefore, the point of y-intercept is \[(0,-2)\].
Now, we have to find the x-intercept. It is a point that the equation makes with the x-axis. At that point \[y=0\]. So, to find the x-intercept, we will put \[y=0\] in the given quadratic equation. We have,
\[-3{{x}^{2}}+3x-2=0\]
Since we cannot factor it, we will use discriminant, we get,
\[D={{b}^{2}}-4ac\]
\[D={{(3)}^{2}}-4(-3)(-2)\]
\[D=9-24\]
\[D=-15<0\]
Since, the value is less than zero, we will not have any real roots for the given quadratic equation. Therefore, the equation does not have a x – intercept.
The graph of the given equation is as follows:

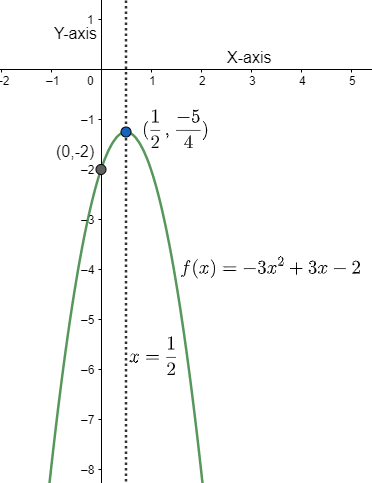
Note:
The line of symmetry and vertex are related. In the above question, we had the parabola opening toward the negative y-axis, so the line of symmetry was similar to the x-coordinate of the vertex. But if we had the parabola opening towards the x-axis, then the line of symmetry would be the y-coordinate of the vertex.
Also, since the above question involves multiple properties to be found. Therefore, it should be done neatly and in an organized manner.