Question

Find equivalent resistance between X and Y.

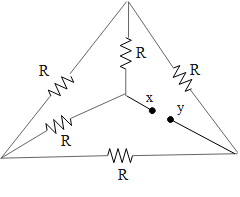
A)$R$
B)$\dfrac{R}{L}$
C)$2R$
D)$5R$

Answer 1

Hint: In the above question, we are asked to obtain the net resistance between x and y. First we need to obtain the equivalent circuit diagram of the above circuit such that we are in a position to figure out how the resistances are in series and parallel with respect to each other. Once we figure that out we can accordingly consider the resistances to be in series and parallel and accordingly determine the equivalent resistance.

Formula used:
${{R}_{Series}}={{R}_{1}}+{{R}_{2}}$
$\dfrac{1}{{{R}_{Parallel}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$


Complete step-by-step solution:
First let us draw the equivalent circuit of the given circuit diagram.

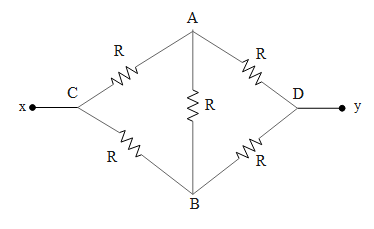
From the above circuit diagram we can conclude that this circuit represents a Wheatstone bridge. The current through the resistance in a Wheatstone bridge is zero, if the resistance in the arm AC i.e. ${{R}_{AC}}$, resistance in the arm AD i.e. ${{R}_{AD}}$, resistance in the arm AB i.e. ${{R}_{CB}}$, resistance in the arm DB i.e.${{R}_{DB}}$ satisfy the condition,
$\dfrac{{{R}_{AC}}}{{{R}_{CB}}}=\dfrac{{{R}_{AD}}}{{{R}_{DB}}}$
Since all the resistors in the circuit have resistance equal to R, from the above condition we get,
$\begin{align}
  & \dfrac{{{R}_{AC}}}{{{R}_{CB}}}=\dfrac{{{R}_{AD}}}{{{R}_{DB}}} \\
 & \Rightarrow \dfrac{R}{R}=\dfrac{R}{R}=1 \\
\end{align}$
Since the above condition is satisfied, there will be no flow of current across the resistor R in arm AB.
If two resistors ${{R}_{1}}\text{ }and\text{ }{{R}_{2}}$ are connected in series, than the equivalent resistance is given by,
${{R}_{Series}}={{R}_{1}}+{{R}_{2}}$
Similarly is the two resistances are connected in parallel, the equivalent resistance is given by,
$\dfrac{1}{{{R}_{Parallel}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
In the above circuit diagram, the resistors in arm CD through point A and across the same arm but through pint B can be treated to be in series. Hence the equivalent resistances across these two arm is equal to,
$\begin{align}
  & {{R}_{Series}}={{R}_{1}}+{{R}_{2}} \\
 & \because {{R}_{Series}}={{R}_{CAD}},\text{ }{{R}_{1}}={{R}_{2}}=R \\
 & \Rightarrow {{R}_{CAD}}=R+R \\
 & \therefore {{R}_{CAD}}=2R \\
\end{align}$
Similarly the resistance in arm CBD is equal to,
$\begin{align}
  & {{R}_{Series}}={{R}_{1}}+{{R}_{2}} \\
 & \because {{R}_{Series}}={{R}_{CBD}},\text{ }{{R}_{1}}={{R}_{2}}=R \\
 & \Rightarrow {{R}_{CBD}}=R+R \\
 & \therefore {{R}_{CBD}}=2R \\
\end{align}$
The above resistances are in parallel with respect to each other. Hence the equivalent resistance ${{R}_{Eq}}$between x and y in the above given circuit is equal to,
$\begin{align}
  & \dfrac{1}{{{R}_{Parallel}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}} \\
 & {{R}_{Parallel}}={{R}_{Eq}},\text{ }{{R}_{CAD}}={{R}_{CBD}}=2R \\
 & \Rightarrow \dfrac{1}{{{R}_{Eq}}}=\dfrac{1}{{{R}_{CAD}}}+\dfrac{1}{{{R}_{CBD}}} \\
 & \Rightarrow \dfrac{1}{{{R}_{Eq}}}=\dfrac{1}{2R}+\dfrac{1}{2R}=\dfrac{1}{R} \\
 & \therefore {{R}_{Eq}}=R \\
\end{align}$
Therefore the correct answer of the above question is option A.

Note: It is to be noted that the complex looking circuits can be reduced by considering the resistances to be either series or parallel. The net resistance in the circuit reduces if the individual resistors are connected in series and increases if connected in parallel. But the current in the circuit across the individual resistors in case of series is the same but parallel it varies.