Question

Find current through $12\Omega $ resistor in Fig

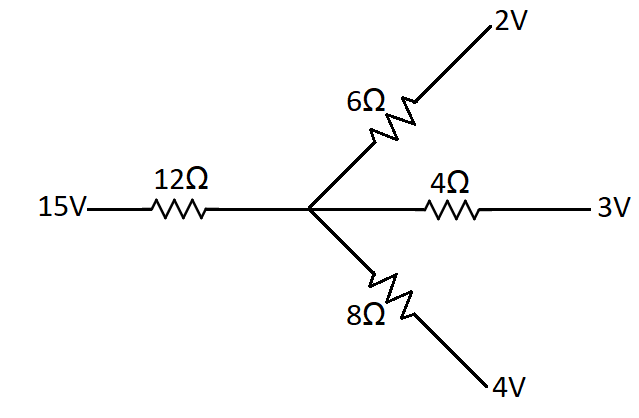
(A) $\dfrac{{52}}{{60}}A$
(B) $\dfrac{{41}}{{60}}A$
(C) $\dfrac{{21}}{{40}}A$
(D) $\dfrac{{23}}{{40}}A$

Answer 1

Hint
We need to first find the voltage at the node in the middle by using Kirchhoff's current law by equating the current from all the sources. Now using that voltage we can find the drop across the $12\Omega $ resistor. With the potential drop and the resistance value we can find the current.

Formula Used: In this solution we will be using the following formula,
$I = {I_1} + {I_2} + {I_3} + ...$ where the $I$s are the current in the different wires across a node.
$V = IR$ where $V$ is the voltage, $R$ is the resistance and $I$ is the current.

Complete step by step answer
In the given circuit, let us name the point in the middle as A and the current in the different wires as ${I_1}$,${I_2}$, ${I_3}$ and $I$ as in the figure below.

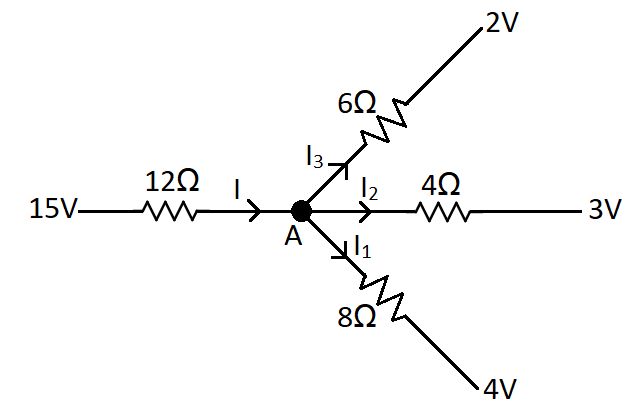
Now according to the Kirchhoff’s Current Law, at the node A the sum of the currents entering will be equal to the sum of the currents leaving. Therefore, we have,
$I = {I_1} + {I_2} + {I_3}$……(1)
Let us consider the potential at the point A be $V$. So the current $I$ will be given by the potential drop across the $12\Omega $ resistor divided by the value of the resistance.
Therefore, $I = \dfrac{{15 - V}}{{12}}$
Similarly, the current ${I_1}$ will be the potential across the $8\Omega $ resistor will be the potential drop divided by the resistance,
${I_1} = \dfrac{{V - 4}}{8}$
For the current given as ${I_2}$ the value will be,
${I_2} = \dfrac{{V - 3}}{4}$
And for the current ${I_3}$ we get,
${I_3} = \dfrac{{V - 2}}{6}$
Now from the equation (1), we have,
$I = {I_1} + {I_2} + {I_3}$
So substituting the values we get,
$\dfrac{{15 - V}}{{12}} = \dfrac{{V - 4}}{8} + \dfrac{{V - 3}}{4} + \dfrac{{V - 2}}{6}$
In the RHS we take the LCM as 24. So we get,
$\dfrac{{15 - V}}{{12}} = \dfrac{{3\left( {V - 4} \right) + 6\left( {V - 3} \right) + 4\left( {V - 2} \right)}}{{24}}$
We can cancel the 12 from denominator of both the sides and doing cross multiplication have,
$2\left( {15 - V} \right) = 3\left( {V - 4} \right) + 6\left( {V - 3} \right) + 4\left( {V - 2} \right)$
On opening the brackets we get,
$30 - 2V = 3V - 12 + 6V - 18 + 4V - 8$
On keeping the terms containing $V$ on one side we get,
$3V + 6V + 4V + 2V = 12 + 18 + 8 + 30$
On doing the addition we get,
$15V = 68$
Hence we get the value of the potential at A as,
$V = \dfrac{{68}}{{15}}V$
Now substituting this value in the equation for current through the $12\Omega $ we get,
$I = \dfrac{{15 - \dfrac{{68}}{{15}}}}{{12}}$
Taking LCM as 15 in numerator we get,
$I = \dfrac{{\dfrac{{225 - 68}}{{15}}}}{{12}}$
Simplifying we get,
$I = \dfrac{{10.46}}{{12}}A$
On multiplying 5 on both the numerator and the denominator we get,
$I = \dfrac{{52.33}}{{60}}A$
We can write this as equivalent to,
$I = \dfrac{{52}}{{60}}A$
Therefore option A is correct.

Note
The Kirchhoff’s current law deals with the conservation of charge that is entering and leaving a junction. It states that the total current that is entering a circuit’s junction is equal to the total current that is leaving the same junction.