Question

Find common tangent of ${x^2} + {y^2} = 4$ and $2{x^2} + {y^2} = 2$ is,

Answer 1

Hint: We will first try to plot the graph of the two curves and then prove that if there is no point of contact then there will be no common tangent between the two given curves.

Complete Step-by-step Solution
Plot the equations ${x^2} + {y^2} = 4$ and $2{x^2} + {y^2} = 2$ in X-axis and Y-axis.

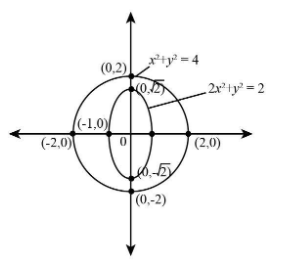
Since, in the diagram it is clear that equation ${x^2} + {y^2} = 4$represents a circle because the equation of circle is ${x^2} + {y^2} = {r^2}$.
Now, we can calculate the radius of the circle by equating the above two equations, we get the value as,
$\begin{array}{c}
{r^2} = 4\\
r = 2
\end{array}$
The circle has a centre at origin and radius 2 units.
We know that the general equation of ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$. The equation $2{x^2} + {y^2} = 2$ represents an ellipse whose major axis is Y-axis and minor axis is X-axis.
The ellipse will cut Y-axis at,
 $\left( {0, - \sqrt 2 } \right)$ and $\left( {0,\sqrt 2 } \right)$
The ellipse will cut X-axis at points
\[\left( { - 1,0} \right)\] and \[\left( {1,0} \right)\]
On comparing the above equations, we will get the value of a and b as,
$\begin{array}{c}
a = 1\\
b = \sqrt 2
\end{array}$
Thus, we can see that the given circle and ellipse have no common tangent. The centre of the circle as well as the ellipse is the origin and the radius of the circle is $2$ and the ellipse has $a = 1$ and $b = \sqrt 2 $. The radius of the circle is greater than the ellipse.
Therefore, there is no common tangent.

Note: General equation for a circle is ${(x - h)^2} + {(y - k)^2} = {r^2}$, where (h, k) is the centre and r is the radius. General equation for ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ where, $a$ represents length from origin to ellipse on X-axis and $b$ represents the length from origin to ellipse on Y-axis