Question

Find area of triangle with base 12cm and altitude 10cm.

Answer 1

- Hint: In this question we are going to solve the problem by putting the values of base and height in the formula of area of the triangle. And the formula is written below.
Here, the given is,
Base of the triangle 12cm.
Altitude of the triangle 10cm.
Formula for area of triangle is,
Area of triangle= $\dfrac{1}{2} \times b \times h$
Where b is the base of the triangle and h is the height of the triangle.

Formula Used:
The formula for calculation volume of cone is =$\dfrac{1}{3}\pi {r^2}h$
Where r is the radius of the cone and h is the height of the cone
And the value of pie is taken as $\dfrac{22}{7}$
For converting the volume into liters we use the conversion
$1c{m^3} = 0.001litre$

Complete step-by-step solution :

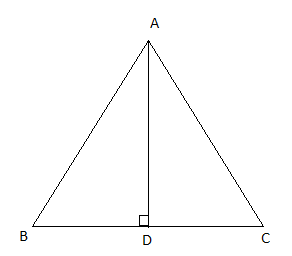
First we will make diagram for better understanding
Draw a triangle ABC with base as BC
Now, from vertices A draw a perpendicular to base BC and where it cuts BC name that point as D
In diagram BC is the base which is given 12cm and AD as altitude or height which is 10cm
Now the putting the values in formula for calculating area of triangle that is stated above
Area of triangle =$\dfrac{1}{2} \times BC \times AD$
Now putting the values of BC and AD we get,
Area of triangle =$\dfrac{1}{2} \times 12 \times 10$
Now for solving we multiply 12 and 10 first, we get
=$\dfrac{1}{2} \times 120$
Now dividing numerator and denominator by 2, we get,
=$60c{m^2}$
Hence the area of triangle is $60c{m^2}$

Note:
Use the correct formula for finding the area of the triangle, by putting the values in the formula and note that for this type of question always make a diagram first for better understanding. By seeing the question we have to analyze what is given and what to find in the problem.