Question

How do you find an equation in standard form of the parabola passing through the points $\left( 1,1 \right)$, $\left( -1,-3 \right)$, $\left( -3,1 \right)$?

Answer 1

Hint: In this problem we need to calculate the equation of the parabola which passes through the given points. We have the standard equation of the parabola as $y=a{{x}^{2}}+bx+c$. So, we will substitute the given points in the standard form of the parabola and simplify the equation to get the system of linear equations in three variables $a$, $b$, $c$. Now we will solve the obtained system of linear equations and substitute the values of $a$, $b$, $c$ in the standard form of the parabola to get the required solution.

Complete step by step solution:
Given points, $\left( 1,1 \right)$, $\left( -1,-3 \right)$, $\left( -3,1 \right)$.
We have the standard form of the parabola as $y=a{{x}^{2}}+bx+c$.
Substituting the first point $\left( 1,1 \right)$ in the above equation, then we will get
$\begin{align}
  & \Rightarrow 1=a{{\left( 1 \right)}^{2}}+b\left( 1 \right)+c \\
 & \Rightarrow a+b+c=1....\left( \text{i} \right) \\
\end{align}$
Substituting the second point $\left( -1,-3 \right)$ in the equation of the parabola, then we will have
$\begin{align}
  & \Rightarrow -3=a{{\left( -1 \right)}^{2}}+b\left( -1 \right)+c \\
 & \Rightarrow a-b+c=-3....\left( \text{ii} \right) \\
\end{align}$
Substituting the third point $\left( -3,1 \right)$ in the equation of the parabola, then we will get
$\begin{align}
  & \Rightarrow 1=a{{\left( -3 \right)}^{2}}+b\left( -3 \right)+c \\
 & \Rightarrow 9a-3b+c=1....\left( \text{iii} \right) \\
\end{align}$
We have the three linear systems of equations in terms of $a$, $b$, $c$. To solve these equations, we are going to eliminate the term $c$ from all the equation by subtracting $\left( \text{i} \right)$ from $\left( \text{ii} \right)$ and $\left( \text{iii} \right)$.
Subtracting $\left( \text{i} \right)$ from $\left( \text{ii} \right)$, then we will have
$\begin{align}
  & \Rightarrow a-b+c-\left( a+b+c \right)=-3-1 \\
 & \Rightarrow a-b+c-a-b-c=-4 \\
 & \Rightarrow -2b=-4 \\
\end{align}$
Dividing the above equation with $-2$ on both sides, then we will get
$\begin{align}
  & \Rightarrow \dfrac{-2b}{-2}=\dfrac{-4}{-2} \\
 & \Rightarrow b=2 \\
\end{align}$
Subtracting equation $\left( \text{i} \right)$ from $\left( \text{iii} \right)$, then we will have
$\begin{align}
  & \Rightarrow 9a-3b+c-\left( a+b+c \right)=1-1 \\
 & \Rightarrow 9a-3b+c-a-b-c=0 \\
 & \Rightarrow 8a-4b=0 \\
\end{align}$
Substituting the value of $b=2$ in the above equation, then we will get
$\begin{align}
  & \Rightarrow 8a-4\left( 2 \right)=0 \\
 & \Rightarrow 8a=8 \\
 & \Rightarrow a=1 \\
\end{align}$
Up to now we have the values of $a=1$, $b=2$. To calculate the value of $c$ we can substitute the known values in any one of the equations we have.
Substituting the values $a=1$, $b=2$ in the equation $\left( \text{i} \right)$ and simplifying it, then we will get
$\begin{align}
  & \Rightarrow a+b+c=1 \\
 & \Rightarrow 1+2+c=1 \\
 & \Rightarrow c=1-3 \\
 & \Rightarrow c=-2 \\
\end{align}$
Substituting the values $a=1$, $b=2$ and $c=-2$ in the standard form of the parabola, then we will get the equation of required parabola as
$\begin{align}
  & \Rightarrow y=\left( 1 \right){{x}^{2}}+\left( 2 \right)x-2 \\
 & \therefore y={{x}^{2}}+2x-2 \\
\end{align}$
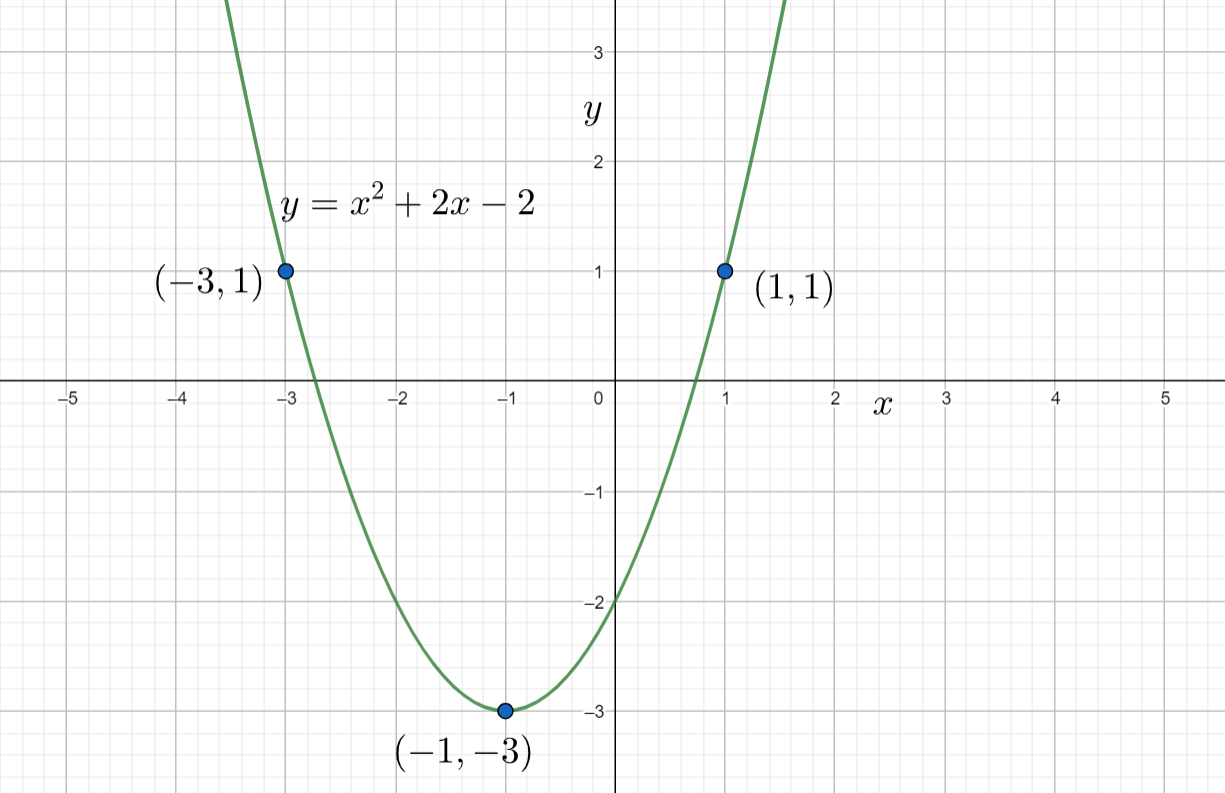
Hence the equation of the parabola passing through the given points $\left( 1,1 \right)$, $\left( -1,-3 \right)$, $\left( -3,1 \right)$ is $y={{x}^{2}}+2x-2$. The graph of the parabola will be

Note:
In this type of problems students may make mistakes at substituting the given points in the standard form of the equation. If the point $\left( {{x}_{1}},{{y}_{1}} \right)$ lies on the parabola, then the equation of parabola must be satisfied by the point $\left( {{x}_{1}},{{y}_{1}} \right)$ i.e., ${{y}_{1}}=a{{x}_{1}}^{2}+b{{x}_{1}}+c$. Students may write the equation as ${{x}_{1}}=a{{y}_{1}}^{2}+b{{y}_{1}}+c$ in hurry but it not the correct way to solve the problem.