Question

How do you find absolute minimum and maximum in calculus?

Answer 1

Hint: We first explain the concept and then take an example of $f\left( x \right)=-{{x}^{3}}-6{{x}^{2}}-9x-2$. We equate it with 0. Extremum points in a curve have slope value 0. We solve the quadratic solution to find the coordinates and the points.

Complete step by step answer:
To find the extremum points we need to find the slope of a function and also the value of the point where the slope will be 0. Extremum points in a curve have slope value 0.
The slope of the function can be found from the derivative of the function ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]$
We now take an example to understand the concept better. We find the relative extrema of the function $f\left( x \right)=-{{x}^{3}}-6{{x}^{2}}-9x-2$.

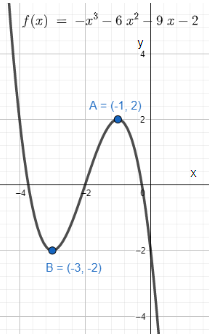
We differentiate both sides of the function $f\left( x \right)=-{{x}^{3}}-6{{x}^{2}}-9x-2$ with respect to $x$.
$\begin{align}
  & f\left( x \right)=-{{x}^{3}}-6{{x}^{2}}-9x-2 \\
 & \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]=\dfrac{d}{dx}\left[ -{{x}^{3}}-6{{x}^{2}}-9x-2 \right] \\
\end{align}$.
We know that the differentiation form for ${{n}^{th}}$ power of $x$ is $\dfrac{d}{dx}\left[ {{x}^{n}} \right]=n{{x}^{n-1}}$.
Therefore, ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( -{{x}^{3}} \right)+\dfrac{d}{dx}\left( -6{{x}^{2}} \right)+\dfrac{d}{dx}\left( -9x \right)+\dfrac{d}{dx}\left( -2 \right)=-3{{x}^{2}}-12x-9$.
To find the $x$ coordinates of the extremum point we take $-3{{x}^{2}}-12x-9=0$.
Solving the given quadratic equation
$\begin{align}
  & -3{{x}^{2}}-12x-9=0 \\
 & \Rightarrow {{x}^{2}}+4x+3=0 \\
\end{align}$
We know for a general equation of quadratic $a{{x}^{2}}+bx+c=0$, the value of the roots of x will be $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$.
In the given equation we have ${{x}^{2}}+4x+3=0$. The values of $a,b,c$ is $1,4,3$ respectively.
We put the values and get $x$ as $x=\dfrac{-4\pm \sqrt{{{4}^{2}}-4\times 1\times 3}}{2\times 1}=\dfrac{-4\pm \sqrt{4}}{2}=\dfrac{-4\pm 2}{2}=-1,-3$.
Therefore, from the value of the $x$ coordinates of the extremum points, we find their $y$ coordinates.
We put values of $x=-1,-3$ in $f\left( x \right)=-{{x}^{3}}-6{{x}^{2}}-9x-2$.
For $x=-1$, the value of \[y=f\left( -1 \right)=-{{\left( -1 \right)}^{3}}-6{{\left( -1 \right)}^{2}}-9\left( -1 \right)-2=2\].
For $x=-3$, the value of \[y=f\left( -3 \right)=-{{\left( -3 \right)}^{3}}-6{{\left( -3 \right)}^{2}}-9\left( -3 \right)-2=-2\].
Therefore, the extremum points are $\left( -1,2 \right);\left( -3,-2 \right)$.

Note: We also can find which point is maxima and minima by finding ${{f}^{''}}\left( x \right)=\dfrac{d}{dx}\left[ {{f}^{'}}\left( x \right) \right]$. If for $x=a,b$, we find ${{f}^{''}}\left( x \right)$ being negative value then the point is maxima and ${{f}^{''}}\left( x \right)$ being positive value then the point is minima.
For ${{f}^{'}}\left( x \right)=-3{{x}^{2}}-12x-9$, we get ${{f}^{''}}\left( x \right)=-6x-12$.
At $x=-1$, ${{f}^{''}}\left( -1 \right)=-6<0$. The point $\left( -1,2 \right)$ is maxima.
At $x=-3$, ${{f}^{''}}\left( -3 \right)=6>0$. The point $\left( -3,-2 \right)$ is minima.