Question

Fill in the blanks with correct word(S) to make the statement true:
Radius of a circle is one half of its ____________ .

Answer 1

Hint: The Diameter is double the radius in a circle. Radius in a circle Is the distance from the centre of the circle to its boundary.

Complete step-by-step answer:
We need to find out the radius of a circle is half of which other property of a circle. Let us draw a circle.

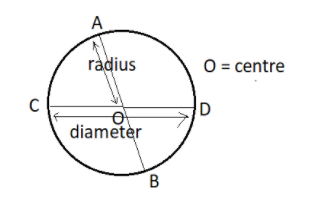
Now, in a circle the radius is the length or the distance from the centre to the boundary of the circle. From the figure radii are $OA,OB,OC and OD$. We know that all radii in a circle are of equal length. So then $OA = OB = OC = OD$ .
The lines drawn in a circle, passing through the centre of the circle, joining two points across the boundaries are all diameters. For the circle given in the figure the diameters are AB and CD and we can see that $AB = AO + OB$.
Since, al radii are equal as established above already, we can say that
$
  AB = AO + AO \\
   \Rightarrow AB = 2AO \\
  Or,\dfrac{{AB}}{2} = AO \\
   \Rightarrow AO = \dfrac{{AB}}{2} \\
$
That is the diameter is twice the radius or that the radius is half the diameter.
Or, each diameter is made of 2 radii. That Is why the diameter is twice the radius, which is another way of saying that radius is half the diameter.
Therefore, the radius is half the diameter.
So we will fill the blank with the word, Diameter.

Note: In a circle a diameter is a special case of chord. A chord is drawn to join any two points on the opposite ends of a circle. It is only when a chord is drawn in such a way that it passes through the centre, that is called a diameter. The radius however does not qualify as a chord, since only one end of the chord lies on the boundary while the other end point lies on the centre.