Question

Fill in the blanks: 1 crore = ………… million.

Answer 1

Hint: We need to follow the conversions of the decimal number system from the Indian decimal system to the International decimal system in powers of 10 from one number to another . While crore belongs to the Indian number system, million belongs to the International number system.

Complete step-by-step answer:
In this question, we need to find out the relation between crore and million. While crore is a number in the Indian number system. million is a number in the International number system. Now let us understand the conversion of International system to Indian number system from the table:

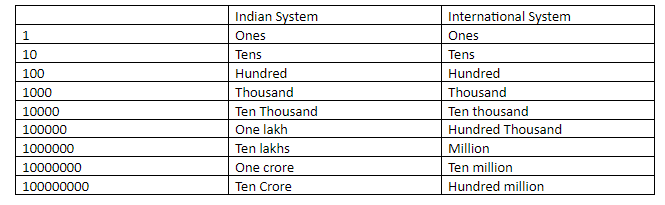
So, clearly from the table,
1 crore = 1 followed by 7 zeroes, 1 crore $ = 10000000$ .
Also from the table:
1million = 1 followed by 6 zeros,
And, 1 0million = 1 million multiplied with 10
That is, $1000000 \times 10$ , which will become 1 followed by 7 zeroes,
so 10 million $ = 10000000$
Which can also be written as 10,000,000 that is ten thousand thousands according to the international number system.
Or, in the Indian System as 1,00,00,000 which is 1 crore.
Therefore we conclude that 10 million as per the International system is the same as 1 crore as per the Indian number system.
Or, 1 crore as per the Indian number system is equal to 10 million as per the International number system.
Hence, 1 crore = 10 million.
So we will fill the blank with the word ten or the number 10.

Note: We have to be extra cautious while putting the zeroes during the conversion of the international number to the Indian number system, since the misplacement of even one zero will change the number completely. Also, we need to be careful with the placing of periods in different number systems. While in the International system the periods are placed at intervals of every three places going left, starting with the hundreds place on the right ; the Indian system places only the first period after the hundreds place starting from right, going to left; the subsequent periods are placed at an interval of two decimal places each towards left after the hundreds place. For example a number say, 234156 when written in the international system will be written as 234,156 while in the Indian system it will be written as 2,34,156.