Question

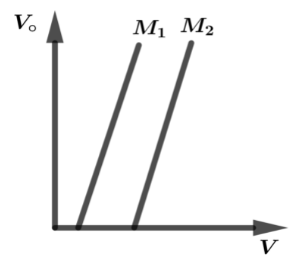
Figure shows variation of stopping potential $\left( {{V_ \circ }} \right)$ with the frequency $\left( V \right)$ for two photosensitive materials ${M_1}$ and ${M_2}$
(i) Why is the slope same for both lines?
(ii) For which material will the emitted electrons have greater kinetic energy for the incident radiation of the same frequency? Justify your answer.

Answer 1

Hint:In the question and figure shows the variation of two slopes in that we have to find out that the two slopes have the same both lines are not. In the second condition we have to prove that the emitted electrons have greater kinetic energy for the incident radiation are not. For this process we have to use the condition of the Einstein equation.

Complete answer:
(i) We have drawn a graph between stopping potential $\left( {{V_ \circ }} \right)$ and frequency $\left( V \right)$. In that graph we have drawn two slopes equally ${M_1}$ and ${M_2}$. The slope stopping potential $\left( {{V_ \circ }} \right)$ versus frequency $\left( V \right)$ is equal to $\left( {\dfrac{h}{e}} \right)$ the universal constant, so the slope is same for both lines. Thus it doesn’t depend on the material.

(ii) The threshold frequency $\left( {{V_ \circ }} \right)$ is lesser for the slope ${M_1}$, so that the kinetic energy is greater for ${M_1}$ in same frequency $\left( V \right)$. Thus the kinetic energy is, $K.E = hV - h{V_ \circ }$. Emitted electrons are greater energy so, $\phi_0 = h{V_ \circ }$ which has lower energy material ${M_1}$. Thus the given two conditions are satisfied in the slope potential difference and frequency.

Note: For two photosensitive materials the same for both the lines. In kinetic energy the potential difference and frequency of an incident radiation for the same frequency is also satisfied. As we discussed in the solution part, for this we have used the Einstein condition.