Question

Figure shows spring+ block+ pulley system which is light. The time period of mass would be
A. $2\pi \sqrt {\dfrac{k}{m}} $
B. $\dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} $
C. $2\pi \sqrt {\dfrac{m}{k}} $
D. $\dfrac{1}{{2\pi }}\sqrt {\dfrac{m}{k}} $

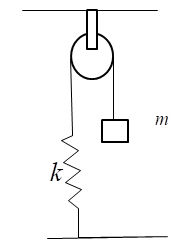
Answer 1

Hint: To solve this type of problems, the first step is to find the mean position of the spring mass system i.e. the natural length of the spring is the position of equilibrium point. Second step is to displace the object from its mean position, the restoring force will act on the body. Third step is to calculate the acceleration of the body and then substitute the value in the formula of time period and proceeding in this manner we will reach our answer.

Complete step-by-step answer:

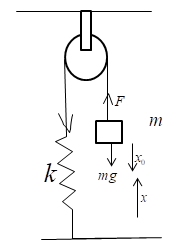
Let in equilibrium position of the block, extension in spring is ${x_0}$
$F = K{x_0}................\left( 1 \right)$
Also at the equilibrium position, the force balances the spring force is gravitational force
Therefore
$F = k{x_0} = mg$
Displace the block by x in the downward direction, the net force on the block will be towards mean position is
\[
  {F_{net}} = kx + F - mg \\
  {F_{net}} = k\left( {x + {x_0}} \right) - mg\,\,\,\,\,\,\,\,\,\,\,\,\left[ {{\text{using equation 1}}} \right] \\
\]
The net force on the block is
${F_{net}} = ma$
Substitute this value in the above equation, we get
\[
   \Rightarrow ma = k\left( {x + {x_0}} \right) - mg \\
   \Rightarrow ma = kx + k{x_0} - mg\,\,\,\,\left[ {\therefore k{x_0} = mg} \right] \\
   \Rightarrow ma = kx \\
   \Rightarrow a = \dfrac{{kx}}{m} \\
\]
The relation between acceleration and angular velocity is given as
${\omega ^2}x = a$
Substituting the value of in the above relation, we get
$
  {\omega ^2}x = \dfrac{{kx}}{m} \\
  \omega = \sqrt {\dfrac{k}{m}} \\
$
The relation between $\omega $ and time period is given as
$T = \dfrac{{2\pi }}{\omega }$
Substituting the value of $\omega $ in the above expression, we get
$T = 2\pi \sqrt {\dfrac{m}{k}} $
Since, the net force acting on the particle is towards mean position and is also proportional to x. Therefore the particle would perform S.H.M and the time period is given by
$T = 2\pi \sqrt {\dfrac{m}{k}} $
Hence, the correct option is C.

Additional information- Simple Harmonic Motion or SHM is characterized as a motion in which the force of restoration is directly proportional to the body's displacement from its mean location. All Simple Harmonic Motions are oscillatory, but not all oscillatory motions are SHM as well as periodic. Oscillatory motion is also called the harmonic motion of all oscillatory movements, in which the most important is simple harmonic motion.

Note: As the block is left hang it will experience a constant downward force by the earth. At the same time it will also experience a force (that will be variable in magnitude as well as direction )by the spring. Thus as a whole it will start doing simple harmonic motion at some mean point with some amplitude.