Question

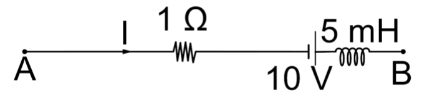
Figure shows part of a circuit. If $I{\text{ }} = {\text{ }}7{\text{ }}A$ and is decreasing at a constant rate of $500{\text{ }}A/s$, then ${V_B}{\text{ }} - {\text{ }}{V_A}$ is

A. $ - {\text{ }}1.5{\text{ }}V$
B. $2.5{\text{ }}V$
C. \[ - {\text{ }}3.5{\text{ }}V\]
D. \[5.5{\text{ }}V\]

Answer 1

Hint: We will directly form an equation as we move from A to B using the conventions of Kirchhoff’s rule. Then, we will substitute the appropriate values and then evaluate the required solution.

Complete step by step answer:
Firstly we start from point A and we start the equation with ${V_A}$. Then, we move to the resistor and we observe that we are moving with the current in the resistor and thus we will have a potential drop thus, we proceed with ${V_A}{\text{ }} - {\text{ }}IR$.

Now, we reach the cell and we are moving from the negative to the positive end which means we are moving from a point of lower potential to a point of higher potential and thus, we will have a potential lift.Thus, we get
${V_A}{\text{ }} - {\text{ }}IR{\text{ }} + {\text{ }}V$
Then, we reach the inductor and we move along with the current and thus there is a potential drop.Thus, we get
${V_A}{\text{ }} - {\text{ }}IR{\text{ }} + {\text{ }}V{\text{ }} + {\text{ }}L{\text{ }}\dfrac{{dI}}{{dt}}$
Finally, we reach the final point B. Thus, we get
${V_A}{\text{ }} - {\text{ }}IR{\text{ }} + {\text{ }}V{\text{ }} + {\text{ }}L{\text{ }}\dfrac{{dI}}{{dt}}{\text{ }} = {\text{ }}{V_B}$

Further, we rearrange the equation and we get
${V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}V{\text{ }} + {\text{ }}L{\text{ }}\dfrac{{dI}}{{dt}}{\text{ }} - {\text{ }}IR{\text{ }} - - - - - - - {\text{ }}(i)$
Now, we will observe the given values
$V{\text{ }} = {\text{ }}10{\text{ }}V$
$\Rightarrow R{\text{ }} = {\text{ }}1{\text{ }}\Omega $
$\Rightarrow I{\text{ }} = {\text{ }}7{\text{ }}A$
As an inductor opposes the flowing current.
Thus, the value of inductance will be negative.
$L{\text{ }} = {\text{ }} - {\text{ }}5{\text{ }}mH{\text{ }} = {\text{ }} - {\text{ }}5{\text{ }} \times {\text{ }}{10^{ - 3}}{\text{ }}H$
Since, there is a current decay in the inductor. Thus, the value of $\dfrac{{dI}}{{dt}}$ is negative.Thus,
$\dfrac{{dI}}{{dt}}{\text{ }} = {\text{ }} - {\text{ }}5{\text{ }} \times {\text{ }}{10^2}{\text{ }}A/s$

Substituting these values in equation $(i)$, we get
${V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}10{\text{ }} + {\text{ }}\left( {5{\text{ }} \times {\text{ }}{{10}^{ - 3}}} \right){\text{ }} \times {\text{ }}\left( {5{\text{ }} \times {\text{ }}{{10}^2}} \right){\text{ }} - {\text{ }}7{\text{ }} \times {\text{ }}1$
Further, we get
${V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}10{\text{ }} + {\text{ }}25{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }} - {\text{ }}7$
Then, we get
${V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}3{\text{ }} + {\text{ }}2.5$
Finally, we get
$\therefore {V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}5.5{\text{ }}V$

Hence, the correct answer is D.


Note: Students should be very cautious while using the values of inductance and current decay. Students should use the idea of exponents as otherwise, they will arrive into a situation of clumsy calculations.