Question

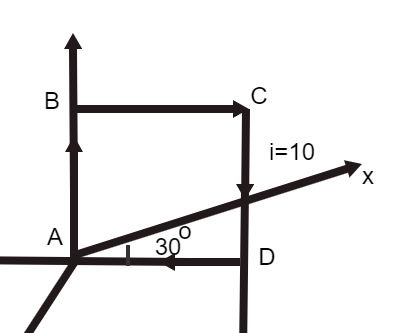
Figure shows a square current-carrying loop ABCD of side \[10\;{\rm{cm}}\] and current \[i = 10\;{\rm{A}}\]. The magnetic moment M of the loop is:

Answer 1

Hint: The above problem can be resolved using the concepts and fundamentals of the magnetic moment, along with the fundamentals of the vector cross product. The magnetic moment is nothing but can be considered as the significant property of any magnetised material which when coming in contact of the magnitude of the external magnetic field, tends to develop a mechanical moment at any point.

Complete step by step answer:
The angle between AD and AX is, \[\theta = 30\;^\circ \].
The length of side is, \[d = 10\;{\rm{cm}} = 10\;{\rm{cm}} \times \dfrac{{1\;{\rm{m}}}}{{100\;{\rm{cm}}}} = 0.1\;{\rm{m}}\].
The magnitude of current is, \[i = 10\;{\rm{A}}\].
The expression for the moment of the loop is,
\[\vec M = i\left( {AD \times AB} \right)\]…………………………………….(1)
The vector AD is given as,
\[\begin{array}{l}
AD = - 2\cos \theta \hat i - 2\sin \theta \hat k\\
AD = - 2\cos 30^\circ \hat i - 2\sin 30^\circ \hat k\\
AD = \left( { - \sqrt 3 \hat i - \hat k} \right).................................................\left( 2 \right)
\end{array}\]
 The vector AB is given as.
\[AB = 2\hat j...............................\left( 3 \right)\]
Solve by substituting the value of equation 2 and 3 in equation 1 as,
\[\begin{array}{l}
\vec M = i\left( {AD \times AB} \right)\\
\vec M = 10\;A\left[ {\left( { - \sqrt 3 \hat i - \hat k} \right) \times \left( {2\hat j} \right)} \right]\\
\vec M = 10\;\left( {2\hat i - 3.46\hat k} \right)\\
\vec M = 20\hat i - 34.6\hat k
\end{array}\]
Therefore, the magnetic moment of the loop is \[20\hat i - 34.6\hat k\].

Note:To resolve the given problem, one must have the basic knowledge about the magnetic moment, along with some knowledge regarding the cross product and dot product. In this problem, the cross product of vectors is used, which needs to be remembered to resolve critical problems in physics. In some aspect, the magnetic moment can also be defined by the orientation of magnet, in the context of which subject magnet or the object tend to generate the magnitude of the external magnetic field. Moreover, the magnetic moment has several practical applications in analysis of magnetic compass, and circuit oriented magnets.