Question

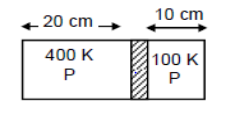
Figure shows a cylindrical tube of length 30 cm which is partitioned by a tight-fitting separator. The separator is very weakly conducting and can freely slide along the tube. Ideal gases are filled in the two parts of the vessel. In the beginning, the temperature in the parts A and B are 400 K and 100 K respectively. The separator slides to a momentary equilibrium position shown in figure. Find the final equilibrium position of the separator, reached after a long time.

Answer 1

Hint: Since, temperatures in the parts A and B are given. At first equilibrium, both side pressures will be the same, and putting combined gas equation of one side of the separating wall,
\[\dfrac{{{P_{{A_1}}} \times {V_{{A_1}}}}}{{{T_{{A_1}}}}} = \dfrac{{{P_{{A_2}}} \times {V_{{A_2}}}}}{{{T_{{A_2}}}}}\] and
at second equilibrium, pressures on both sides will be the same.

Complete step by step answer:
Let the initial pressure of the chambers A and B be \[{P_{{A_1}}}\] and \[{P_{{B_1}}}\], respectively.
Let the final pressure of chambers A and B be \[{P_{{A_2}}}\] and \[{P_{{B_2}}}\], respectively.
Let the Curved Surface Area be A.
\[
  {V_{{A_1}}} = 0.2A \\
  {T_{{A_1}}} = 400K \\
  {V_{{B_1}}} = 0.1A \\
  {T_{{B_1}}} = 100K \\
 \]
At first equilibrium, both side pressures will be the same.
\[{P_{{A_1}}} = {P_{{B_1}}}\]
Let the final temperature at equilibrium be T. Then,
Putting combined gas equation of one side of the separating wall,

\[
  \dfrac{{{P_{{A_1}}} \times {V_{{A_1}}}}}{{{T_{{A_1}}}}} = \dfrac{{{P_{{A_2}}} \times {V_{{A_2}}}}}{T} \\
   \Rightarrow \dfrac{{{P_{{A_1}}} \times 0.2A}}{{400}} = \dfrac{{{P_{{A_2}}} \times {V_{{A_2}}}}}{T} \\
 \]
\[ \Rightarrow {P_{{A_2}}} = \dfrac{{{P_{{A_1}}} \times T \times 0.2A}}{{400 \times {V_{{A_2}}}}}\] … (1)
For second chamber:
\[
  \dfrac{{{P_{{B_1}}} \times {V_{{B_1}}}}}{{{T_{{B_1}}}}} = \dfrac{{{P_{{B_2}}} \times {V_{{B_2}}}}}{T} \\
   \Rightarrow \dfrac{{{P_{{B_1}}} \times 0.1A}}{{100}} = \dfrac{{{P_{{B_2}}} \times {V_{{B_2}}}}}{T} \\
 \]
\[ \Rightarrow {P_{{B_2}}} = \dfrac{{{P_{{B_1}}} \times T \times 0.1A}}{{100 \times {V_{{B_2}}}}}\] … (2)
At second equilibrium, pressures on both sides will be the same
\[
  {P_{{A_2}}} = {P_{{B_2}}} \\
   \Rightarrow \dfrac{{{P_{{A_1}}} \times T \times 0.2A}}{{400 \times {V_{{A_2}}}}} = \dfrac{{{P_{{B_1}}} \times T \times 0.1A}}{{100 \times {V_{{B_2}}}}} \\
   \Rightarrow \dfrac{{{P_{{A_1}}}}}{{2{V_{{A_2}}}}} = \dfrac{{{P_{{B_1}}}}}{{{V_{{B_2}}}}} \\
 \]
\[ \Rightarrow 2{V_{{A_2}}} = {V_{{B_2}}}\] … (3)
Now,
\[{V_{{B_2}}} + {V_{{A_2}}} = 0.3A\]
\[ \Rightarrow 2{V_{{A_2}}} + {V_{{A_2}}} = 0.3A\] (from equation (3))
$
   \Rightarrow 3{V_{{A_2}}} = 0.3A \\
   \Rightarrow {V_{{A_2}}} = 0.1A \\
 $
Let \[{V_{{A_2}}}\] be l A
l = 0.1A
l = 10 CM

Thus, the separator will be at a distance 10 cm from the left end.

Note: The alternate way of solving this problem is,
The final position of the separating wall is at distance x from the left end. So it is at a distance \[(30-x)\] from the right end.
Putting combined gas equation of one side of the separating wall,

$\dfrac{{{P_1} \times {V_1}}}{{{T_1}}} = \dfrac{{{P_2} \times {V_2}}}{{{T_2}}}$
$ \Rightarrow \dfrac{{{P_1} \times 20A}}{{400}} = \dfrac{{{P_2} \times A}}{T}$ … (a)
$ \Rightarrow \dfrac{{{P_1} \times 10A}}{{100}} = \dfrac{{ - {P_2} \times \left( {30 - x} \right)}}{T}$ … (b)
From equation (a) and (b), we get
$
  \dfrac{1}{2} = \dfrac{x}{{30 - x}} \\
   \Rightarrow 30 - x = 2x \\
   \Rightarrow 3x = 30 \\
   \Rightarrow x = 10cm \\
 $