Question

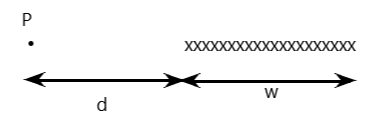
Figure shows a cross section of a long ribbon of width $ \omega $ that is carrying a uniformly distributed total current $ i $ into the page. Calculate the magnitude and direction of the magnetic field $ B $ at a point P in the plane of the ribbon at a distance $ d $ from its edge.

Answer 1

Hint: Since a uniform distribution is involved the current density should be incorporated. Using the expression for the magnetic field for such wires, integrate through the entire width of the wire.

Formula used: In this solution we will be using the following formulae;
 $ dB = \dfrac{{\mu \lambda dx}}{{2\pi x}} $ where $ B $ is the magnetic field, and $ dB $ signifies a differential element of it, $ \mu $ is the permeability of free space, and $ x $ is the position/length in the horizontal axis.
 $ \lambda $ is the line current density and can be defined as $ \lambda = \dfrac{i}{\omega } $ where $ i $ is the current, and $ \omega $ is the width of the wire.

Complete Step-by-Step solution
To solve we recall the biot savart law, which can be described for a wire as
 $ dB = \dfrac{{\mu \lambda dx}}{{2\pi x}} $ where $ B $ is the magnetic field, and $ dB $ signifies a differential element of it, $ \mu $ is the permeability of free space, and $ x $ is the position/length in the horizontal axis, and $ \lambda $ is the current density.
Since the current is unchanging and is uniform, the current density is a constant.
We are to find the magnetic field at distance $ d $ from the wire. To do so, we integrate the above equation from $ d $ to $ d + \omega $ as in
 $ B = \int_d^{d + \omega } {\dfrac{{\mu \lambda dx}}{{2\pi x}}} = \dfrac{{\mu \lambda }}{{2\pi }}\int_d^{d + \omega } {\dfrac{{dx}}{x}} $
By integrating, we have
 $ B = \dfrac{{\mu \lambda }}{{2\pi }}\left[ {\ln x} \right]_d^{d + \omega } $
Carrying out the range, we have that
 $ B = \dfrac{{\mu \lambda }}{{2\pi }}\ln \dfrac{{d + \omega }}{d} $
But $ \lambda $ is the line current density and can be defined as $ \lambda = \dfrac{i}{\omega } $ where $ i $ is the current, and $ \omega $ is the width of the wire.
Hence,
 $ B = \dfrac{{\mu \dfrac{i}{\omega }}}{{2\pi }}\ln \dfrac{{d + \omega }}{d} $
 $ \Rightarrow B = \dfrac{{\mu i}}{{2\pi \omega }}\ln \dfrac{{d + \omega }}{d} $
Using the right hand rule for current, we see that the direction of the magnetic field at point
P is directed upward.

Note
For clarity, as done above, observe that the current density was written finally as $ \dfrac{i}{\omega} $ . This is because in any such question in an exam, the answers must be written in terms of the parameters given. Any incorporated parameters should be defined in terms of given ones.