Question

Figure shows a conducting loop $ABCDA$ placed in a uniform magnetic field (strength $B$) perpendicular to its plane. The part $ABC$ is the (three-fourth) portion of the square of side length $l$. The part $ADC$ is a circular arc of radius $R$. The points $A$ and $C$ are connected to a battery which supplies a current $I$ to the circuit. The magnetic force on the loop due to the field $B$ is:

A. $zero$
B. $BIl$
C. $2BIR$
D. $\dfrac{{BIlR}}{{I + R}}$

Answer 1

Hint: Since, the current through the loop $ABCDA$ splits into to part, one flows through $ABC$ and other through $ADC$. During the current flow, there will be some force generated. To find the total force generated in the loop $ABCDA$, the force generated on loops $ABC$ and $ADC$ are calculated. Since, the two currents travel the same distance in the magnetic field, the current gets added. Thus, the total force can be calculated.

Useful formula:
Relation between force, current and magnetic field will be given by,
$F = BIl$
Where, $F$ is the force on the conductor, $B$ is the magnetic field, $I$ is the current flows through the conductor and $l$ is the length of the conductor.

Complete Step by step solution:

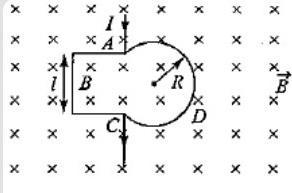
Assume that,
The current through the loop $ABC$ is $I1$
The current through the loop $ADC$ is $I2$
The length where the current flow in loop $ABC$ is ${l_1}$
The length where the current flow in loop $ADC$ is ${l_2}$

The force generated on the loop $ABC$,
${F_{ABC}} = B \times I1 \times {l_1}\;......................................\left( 1 \right)$
Where, ${F_{ABC}}$ is the force generated on loop $ABC$, $I1$ is the current flows through the loop $ABC$ and ${l_1}$ is the length of the loop $ABC$.

The force generated on the loop $ADC$,
${F_{ADC}} = B \times I2 \times {l_2}\;......................................\left( 2 \right)$
Where, ${F_{ADC}}$ is the force generated on loop $ADC$, $I2$ is the current flows through the loop $ADC$ and ${l_2}$ is the length of the loop $ADC$.

Hence, the total force on loop $ABCDA$ is the sum of the force on loop $ABC$ and the force on loop $ADC$,
$F = {F_{ABC}} + {F_{ADC}}..........................................\left( 3 \right)$
Substitute the values of (1) and (2) equation (1),
$
  F = \left( {B \times I1 \times {l_1}} \right) + \left( {B \times I2 \times {l_2}} \right) \\
  F = B\left[ {\left( {I1 \times {l_1}} \right) + \left( {I2 \times {l_2}} \right)} \right] \\
 $

Since, the current travels the same length in the loops $ABC$ and $ADC$ ,
 $l = {l_1} = {l_2}$
Hence,
$
  F = B\left[ {\left( {I1 \times l} \right) + \left( {I2 \times l} \right)} \right] \\
  F = B \times l\left[ {I1 + I2} \right] \\
 $
The total current, $I = I1 + I2$
Thus,
$
  F = B \times l\left[ I \right] \\
  F = BIl \\
 $

Hence, the option (B) is correct.

Note: In the loop $ABCDA$, even the structure of the loops $ABC$ and $ADC$ may vary, but the current flows through the loops in the uniform magnetic field travels the same distance in both the loops. A force will be generated in the current carrying conductor placed in a uniform magnetic field, this is the statement of Faraday’s law of induction. The force generated in the loop $ABCDA$, is the sum of the force generated in loops $ABC$ and $ADC$.