Question

Figure shows a balanced Wheatstone bridge. Now it is disturbed by changing P to $11\omega $. Which of the following steps will not bring the bridge to balance again?

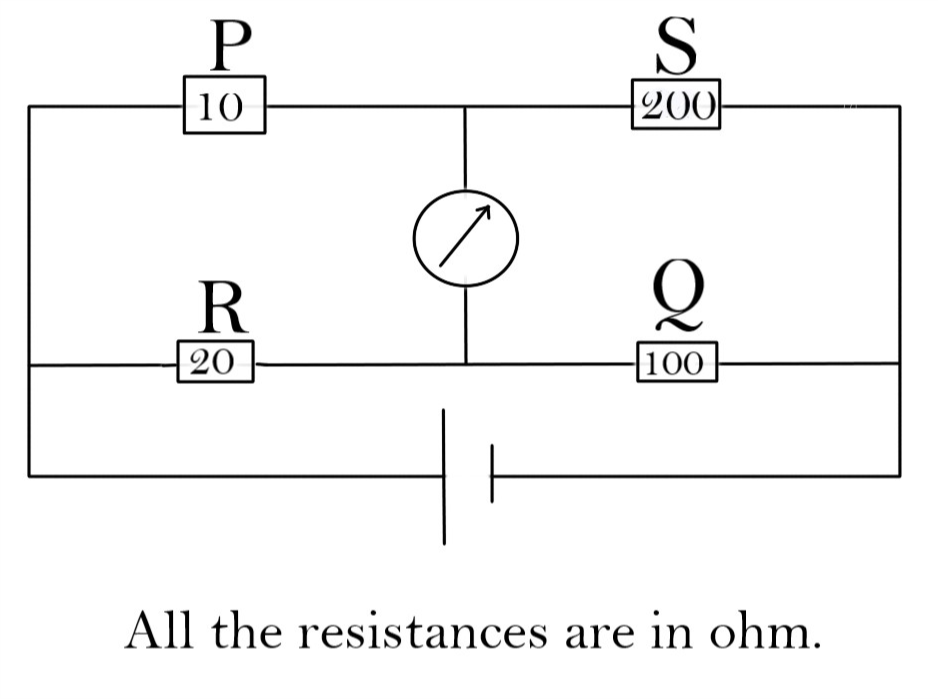
A. Increasing R by $2\Omega $
B. Increasing S by $20\Omega $
C. Increasing Q by $10\Omega $
D. Making product $RQ = 2200({\Omega ^2})$

Answer 1

Hint: Make use of the concept of a balanced Wheatstone bridge.

Step by step answer:
If we increase the value of P from $10\Omega $ to $11\Omega $ then, either P or Q should be increased or S should be decreased. Hence increasing s by any amount will not result in the balancing of the bridge in any way.
We know that,
According to Wheatstone principle,
$\dfrac{P}{Q} = \dfrac{R}{S}$
$PS = RQ$
If we calculate RQ for this circuit,
$RQ = 2200{\Omega ^2}$
So, the equation becomes,
$PS = RQ = 2200{\Omega ^2}$
b) is correct

Additional information:
The device used for the measurement of minimum resistance with the help of comparison method is known as the Wheatstone bridge. The value of unknown resistance is determined by comparing it with the known resistance. The Wheatstone bridge works on the principle of null deflection, i.e. the ratio of their resistances are equal, and no current flows through the galvanometer. The bridge is very reliable and gives an accurate result.

Note: If we replace the resistances in the opposite branches with each other than the Wheatstone bridge still remains balanced and it still holds the Wheatstone’s law.