Question

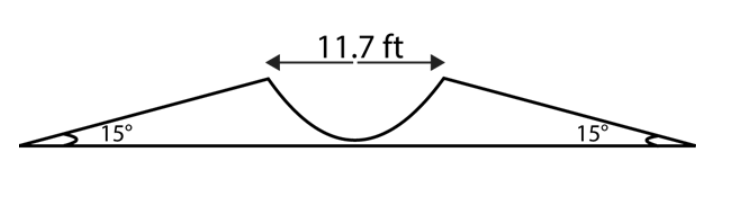
Figure shows a 11.7 ft wide ditch with the approach roads at an angle of 15 degrees with the horizontal. With what minimum speed should a motorbike be moving on the road so that it safely crosses the ditch?

Answer 1

Hint: We have to consider the motorbike to be in a projectile motion initiating at the start of the ditch with the range equal to the width of the ditch i.e. 11.7 ft. Range of a projectile, $R = \dfrac{{{u^2}\sin 2\theta }}{g}$ where u is the initial velocity and $\theta $ is the angle of launch.

Complete step by step solution:
Projectile motion is the motion of an object thrown or projected into the air, under the effect of only the acceleration of gravity.
So here, we can assume the motorbike to be in a projectile motion after it jumps off at the start of the ditch. And because the motion of the motor bike will be a projectile motion after it jumps off at the start of the ditch, the distance covered to cross the ditch safely would be equal to the range of the projectile motion.

Let’s see the information given in the question,
Range, R= 11.7 ft
Angle of projection, $\theta = 15^\circ $
Acceleration due to gravity, $g = 9.8m/{s^2} = 32ft/{s^2}$
Let the velocity of projection be u.
We know that the horizontal range of a projection is given by
\[
  R = \dfrac{{{u^2}\sin 2\theta }}{g} \\
   \Rightarrow 11.7ft = \dfrac{{{u^2}\sin }}{{32ft/{s^2}}} = \dfrac{{{u^2}\sin 30}}{{32}} \\
\]
$ \Rightarrow {u^2} = \dfrac{{11.7 \times 32}}{{\sin 30}}$
$ \Rightarrow {u^2} = 748.8f{t^2}/{s^2}$
$ \Rightarrow u = 27.36ft/s$

Therefore, the minimum speed that the motorbike be moving with to safely cross the ditch is approximately 27ft/s.

Note: We can also convert the ditch width in metres and solve the question in m/s, that entirely depends on the options if the question is in MCQ or it is mentioned in the question to write the final answer in specific units. Also, if the answer differs from the textbook , it might be because the length of motorbike might be given in the question which has to be added in the range/distance to be covered as the rear tyre of the bike has to be on the end of the ditch to cross safely.
Also, here we have to write the equations considering we need the range greater than the width of the ditch. So, all equations can be written with R>=11.7ft.