Question

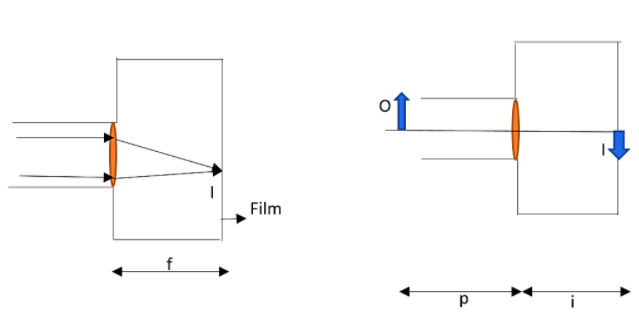
Figure (a) depicts the fundamental structure of an old film camera. A lens can be moved forward or back to create an image on
film at the back of the camera. As shown in the figure, for a particular camera in between the lens and the film set at $f=0.5cm$, parallel light rays from a very distant object $O$ converges to a point image on the film within the distance. The object has been brought nearer to a distance of $p=100cm$and the lens film distance is adjusted so that an inverted real image develops on the film. (a) What is the lens film distance $i$ now? (b) By how much was distance $i$ changed?

Answer 1

Hint: The lens formula has to be used at first to find out the lens film distance. Substitute the values in it. The difference between the focal length of the lens and the distance between the lens films should be taken then. This all will help you in answering this question.

Complete step by step answer:
(a) we have to use the lens formula first. Now, the lens film distance can be shown as,
$i={{\left( \dfrac{1}{f}-\dfrac{1}{p} \right)}^{-1}}$
The focal length of the lens can be mentioned as,
$f=5.0cm$
The distance between the lens films has been adjusted so that an inverted real image forms on the film. It has been given as,
$p=100cm$
Substituting the values in it will give,
\[i={{\left( \dfrac{1}{5.0cm}-\dfrac{1}{100cm} \right)}^{-1}}=5.3cm\]
(b) The variation in the lens-film distance can be found by taking the difference between the focal length of the lens and the distance between the lens films. That is we can write that,
\[i=5.3cm-5.0cm=0.30cm\]
Therefore the answer has been calculated.

Note:
The focal length of a lens is defined as the measure of the strength of the system converges or diverges light. It is defined as the reciprocal of the power of the system. A positive focal length represents a system that converges light. While a negative focal length represents that the system diverges light.