Question

How many faces a cube has?
A. 4
B. 6
C. 8
D. 12

Answer 1

Hint: In this particular question construct a cube and the face of the cube will be the squares formed by the cube. So, observe the cube to find all the square shapes formed in the cube. And count them to find the required number of faces.

Complete step-by-step answer:
Let us draw a cube and name its vertices.

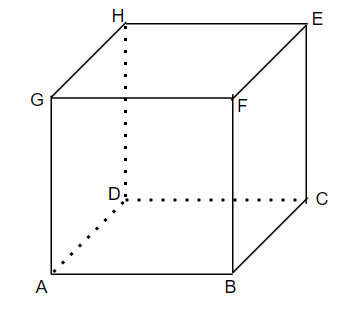
A Cube is a 3-dimensional shape.
And the vertex of the cube is the end point.
So, the vertex in the above drawn cube will be A, B, C, D, E, F, G and H.
So, there are a total of 8 vertices in a cube.
Now the edge is the line formed by joining two adjacent vertices. So, there are 12 such lines (i.e. edges) in a cube.
Hence, the edges of the above cube will be AB, BC, CD, DA, AG, BF, CE, DH, EF, FG, GH and HE.
Now the dotted lines represent the back side of the cube because the cube is a three dimensional solid.
Now the face of the cube is the square formed by joining four continuous vertices.
So, the faces in the above cube must be ABCD, BCEF, EFGH, GHDA, ABFG and CDHE.
So, there are a total of 6 faces in the above cube drawn.
Hence, the cube is a three-dimensional figure bounded by six square faces.

So, the correct answer is “Option B”.

Note: Whenever we face such types of questions then it is important to first, draw the figure of the cube and do proper naming of the end points. And after that recall the definition of vertex, edge and face of a cube. Although these definitions will be the same for most of the shapes like cuboid has same vertex and edges as that of cube but the face of cuboid is a rectangle while cube has square faces. And we should remember that the cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices.