Question

Express in radians and also in degrees the angle of a regular polygon of (i). 40 sides (ii). n sides.

Answer 1

Hint: Try to express the square and regular pentagon in terms of triangles and hence, try to impose the same for a regular polygon with sides 40 and n. Then, find the angle for them in degrees and convert it to radians by using the conversion factor \[\dfrac{\pi }{{180^\circ }}\].

Complete step-by-step answer:
A polygon is a closed figure formed with straight lines.
A regular polygon is a polygon having all of its sides equal and all the angles equal.
The simplest polygon is the triangle and the sum of its angles is 180°.
A four-sided regular polygon is called a square. A square can be expressed as two triangles as shown in the figure. Hence, the sum of the angles of the square is \[2 \times 180^\circ\], which is \[360^\circ \].

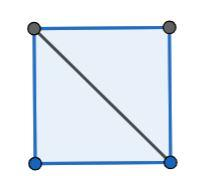
A five-sided regular polygon is called a regular pentagon. A regular pentagon can be expressed as three triangles as shown in the figure. Hence, the sum of the angles is \[3 \times 180^\circ \],which is \[540^\circ \].

Hence, the sum of angles of a regular polygon of 40 sides is \[38 \times 180^\circ \], which is \[6840^\circ \].
Now, each angle is the sum of the total angles divided by the number of sides.
\[\dfrac{{6840^\circ }}{{40}} = 171^\circ \]
Hence, the angle of the regular polygon with 40 sides is 171°.
The sum of angles of an n-sided regular polygon is \[(n - 2) \times 180^\circ \].
The value of each angle is \[(n - 2) \times 180^\circ \] divided by n, which is \[\dfrac{{(n - 2)}}{n} \times 180^\circ \].
To convert from degree to radians, we need to multiply the angle with \[\dfrac{\pi }{{180^\circ }}\].
Hence, the angle of a 40 sided polygon is given as follows:
\[171^\circ \times \dfrac{\pi }{{180^\circ }} = 0.95\pi rad\]
Hence, the angle of an n- sided polygon is given as follows:
\[\dfrac{{n - 2}}{n} \times 180^\circ \times \dfrac{\pi }{{180^\circ }} = \dfrac{{n - 2}}{n}\pi rad\]
Hence, we found the required values.

Note: You can also directly use the formula for the value of the angle of an n-sided polygon which is \[\dfrac{{(n - 2)}}{n} \times 180^\circ \] and use it to find the answers.To convert degree into radians we have to just multiply \[\dfrac{\pi }{{180^\circ }}\] and to convert radians into degree we have to multiply \[\dfrac{180^\circ }{{\pi }}\].