Question

Explain how the formula for the area of a trapezoid is derived from the formula for the area of a triangle?

Answer 1

Hint: Here in this question, we have to derive the formula for the area of the trapezoid by using the area of a triangle. Let us consider the diagram of trapezoid, if we draw a perpendicular line to the trapezoid, we get two triangles and one rectangle. The area of the triangle is given by $ \dfrac{1}{2}b \times h $ , using this we find the area of the trapezoid

Complete step-by-step answer:

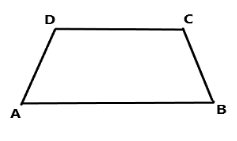
Now consider the trapezoid, here ABCD is a trapezoid which is shown in the figure. In the trapezoid ABCD, the line AB is parallel to the line CD. Where AB is the lower base and CD is an upper base. Now let we draw a diagonal to the trapezoid ABCD. Draw a perpendicular line from a point C and D to the base line AB. Then we get two triangles and one square and using the formula of area of triangle and area of square we can determine the area of the trapezoid.

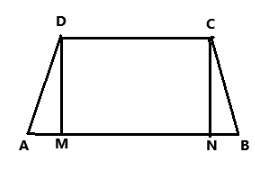
Now let us consider the and draw perpendicular lines. $ DM \bot AB $ and $ CN \bot AB $ . We have two triangles and one square. Now consider the triangle ADM, the area of a $ \vartriangle ADM $ is given by
 $ {A_1} = \dfrac{1}{2}AM \times h $ , where AM is a base and h is height
Now consider the triangle CNB, the area of a $ \vartriangle CNB $ is given by
 $ {A_2} = \dfrac{1}{2}BN \times h $ , where AM is a base and h is height.
Now consider the rectangle DCNM, the area of the rectangle is given by
 $ {A_3} = l \times b = MN \times h $ .
Now the area of the trapezoid is given by
 $ A = {A_1} + {A_2} + {A_3} $ . Therefore, by substituting all the values we get
 $ A = \dfrac{1}{2}AM \times h + \dfrac{1}{2}BN \times h + MN \times h $
On simplifying we get
 $ A = \dfrac{h}{2}\left( {AM + BN + 2MN} \right) $
Hence, we have determined the area of trapezoid by using the area of triangle
So, the correct answer is “ $ A = \dfrac{h}{2}\left( {AM + BN + 2MN} \right) $ ”.

Note: The area of the trapezoid is also determined by using the area of the parallelogram also. Suppose if we draw one diagonal to the trapezoid, we get two triangles and to that two triangles if we draw a perpendicular line we get the area of the triangle. By adding these two areas we can determine the area of a trapezoid.