Question

Explain how a moving coil galvanometer is converted into an ammeter. Derive the necessary formula.

Answer 1

Hint: A galvanometer is a measuring device which can show both the direction and magnitude of electric current whereas an ammeter is a current measuring device that can only show the magnitude of electric current. A galvanometer can also be used to measure voltage.

Complete step by step answer:
A moving coil galvanometer is a highly sensitive electromagnetic device that can detect the currents as low as the order of a few microamperes. The working of the galvanometer is based on the principle that, when a current-carrying coil is placed in an external magnetic field, it experiences some torque.
A galvanometer is a more sensitive device as compared to an ammeter. It cannot measure higher currents because of its sensitivity. Because of its high sensitivity, the needle of the galvanometer will deflect more for smaller currents, hence cannot measure higher currents.

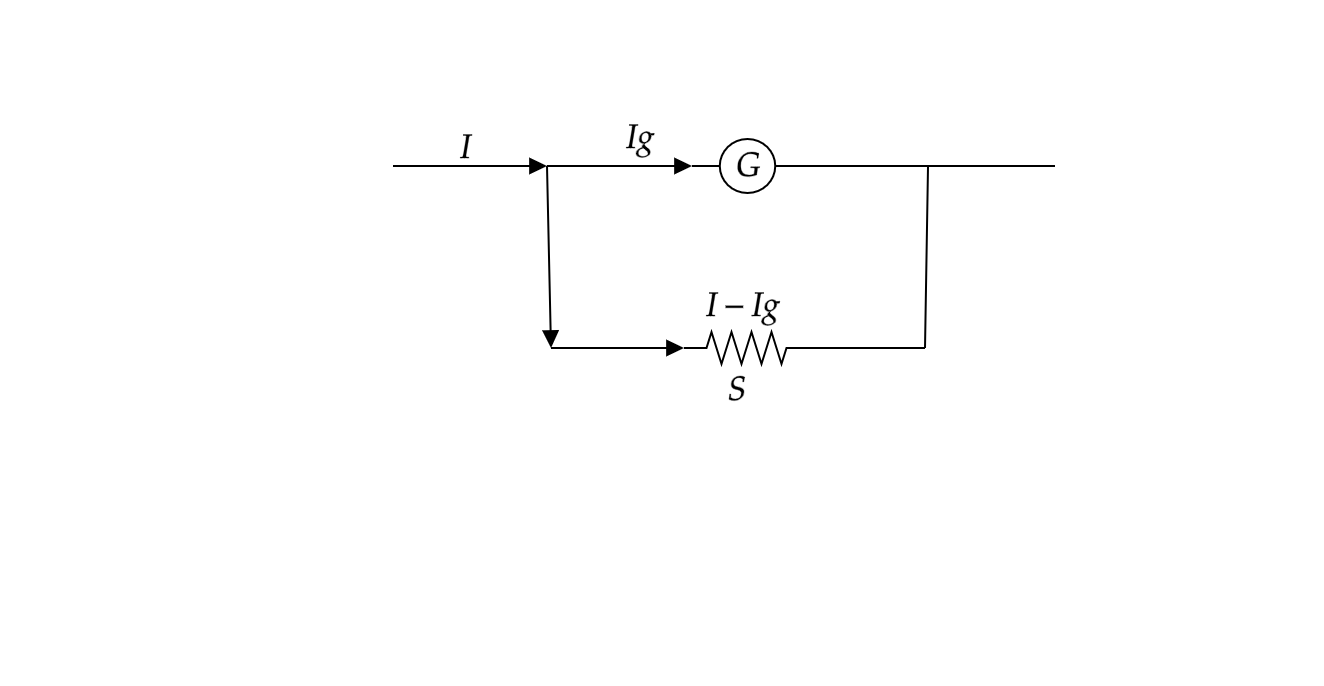
To convert a galvanometer into an ammeter, we must lower the amount of deflection for a given amount of current so that we will be able to measure large amounts of currents. For this to happen, we connect a very low resistance called shunt resistance (denoted by S in the diagram) parallel to the galvanometer. When the current passes through the galvanometer, the value of shunt is adjusted in such a way that most of the current passes through the shunt, and thereby we can measure large amounts of currents from the galvanometer as deflection is reduced.
Required formulae:
In the above circuit diagram,
\[{{R}_{G}}\] is the resistance of the galvanometer
\[I\] is the total current passing in the circuit
\[{{I}_{G}}\] is the current passing through the galvanometer and
\[{{R}_{S}}\] is the shunt resistance
The current passing through the resistance is given by,
\[{{I}_{S}}=I-{{I}_{G}}\]
The conversion formula for a galvanometer into ammeter is:
\[\begin{align}
  & {{R}_{G}}\times {{I}_{G}}={{I}_{S}}\times {{R}_{S}} \\
 & \Rightarrow {{R}_{G}}\times {{I}_{G}}=(I-{{I}_{G}})\times {{R}_{S}} \\
\end{align}\]
This formula follows from application of Coulomb's law, that when voltage is constant, the resistance is inversely proportional to current.

Note: When the above shunt resistance is connected in parallel across the galvanometer, the galvanometer works as an ammeter and when the same shunt resistance is connected in series with the galvanometer, the galvanometer acts as a voltmeter.