Question

Explain (a) How are prisms and cylinders alike?
                                 (b) How are pyramids and cones alike?

Answer 1

Hint: First draw diagrams of the given geometrical structures. Try to relate by increasing the sides in prism with respect to the cylinder and increasing the vase sides of the pyramid with respect to cones.

Complete step-by-step answer:
(a) As we know cylinders and prisms both are solids. So, one similarity will always be there.
Now, we can define a prism as a solid with bases that are polygons and the sides are flat surfaces. Diagram of a prism:-

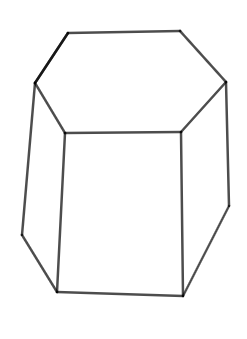
Here, we have 6 sides in the prism above.
A cylinder is one of the most basic curved geometric shapes with surface formed by the points at a fixed distance from a given line segment, known as axis of the cylinder i.e. a solid geometrical figure with straight parallel sides and a circular cross section as shown in diagram below.

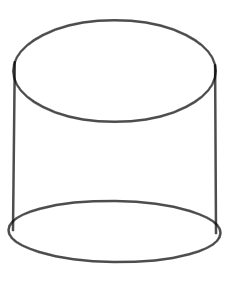
Now, imagine a prism with regular polygons for bases, and as you increase the number of sides, the solid gets to look just like a cylinder.
So, we can say that a cylinder is a prism with an infinite number of faces.
(b) First, let us define pyramids and cones to understand the similarity between them.
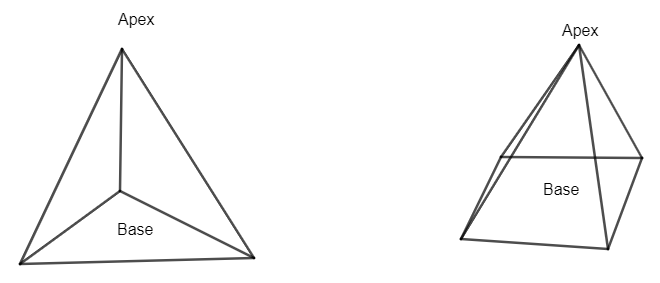
We can define a pyramid as a structure with a square or triangular base and sloping sides that meet in a point at the top, especially one built using stone as a royal tomb in ancient Egypt.
Diagram of pyramid can be given as:

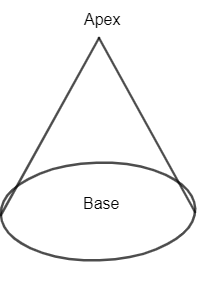
Now, cones can be defined as three-dimensionally geometrical shapes that taper smoothly from a flat base to a point called the apex or vertex.
Diagram of cone can be given as

Now, we can imagine a pyramid with higher base sides. If you increase the number of sides of its base it becomes a cone.
Hence, a cone is termed as a pyramid with infinite base sides.
Note: There is nothing similar in prism and cylinder or cone and pyramid with respect to fundamental properties of them. So, we need to think differently to get similarity between them as given in the solution.
One can go wrong if they try to relate similarity between the figures with respect to surface area or volume of the given diagrams. All of them have different areas and volumes.