Question

How do you expand ${(3x + 2)^3}$ using Pascal’s triangle ?

Answer 1

Hint: For solving this particular question , we have to use the Pascal’s Triangle. Here for expanding ${(3x + 2)^3}$ , we have to use the fourth row with coefficients 1 3 3 1 , with decreasing powers of $3x$ and increasing powers of $2$.

Complete step-by-step solution:
We have given ${(3x + 2)^3}$ ,
We have to expand this using Pascal’s Triangle.
From Pascal's Triangle
Now, using fourth row with coefficients : 1 3 3 1
Here, we have decreasing powers of $3x$ from ${(3x)^3}$to ${(3x)^0}$
and increasing powers of $2$ from ${(2)^0}$ to ${(2)^3}$ .
Now , we can write ,
\[ \Rightarrow {\left( {3x + 2} \right)^3} = 1\times {\left( {3x} \right)^3}\times {\left( 2 \right)^0} + 3\times {\left( {3x} \right)^2}\times {\left( 2 \right)^1} + 3\times {\left( {3x} \right)^1}\times {\left( 2 \right)^2} + 1\times {\left( {3x} \right)^0}\times {\left( 2 \right)^3}\]
\[ \Rightarrow 1\times \left( {27{x^3}} \right)\times 1 + 3\times \left( {9{x^2}} \right)\times 2 + 3\times \left( {3x} \right)\times 4 + 1\times 1\times 8\]
 \[ \Rightarrow 27{x^3} + 54{x^2} + 36x + 8\]
Here, we get the required result.

Thus the correct answer is \[27{x^3} + 54{x^2} + 36x + 8\]

Note: Pascal’s Triangle is very useful when we have to expand a binomial expression.

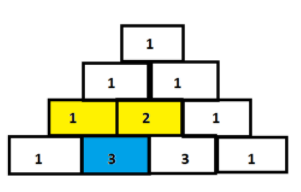
The rows of Pascal's triangle are conventionally enumerated starting with row $n = 0$ highest (the zeroth row). The entries in each row are numbered from the left beginning with $k = 0$ and are usually staggered relative to the numbers within the adjacent rows. Triangulum could also be constructed within the following manner: In row zero (the topmost row), there's a singular nonzero entry one.

Each entry of every subsequent row is made by adding the amount above and to the left with the amount above and to the proper , treating blank entries as zero. for instance , the initial number within the first (or any other) row is one (the sum of zero and one), whereas the number one and three within the third row are added to supply the number four within the fourth row.