
How do you evaluate sine, cosine, tangent of \[\dfrac{\pi }{4}\] without using a calculator?
Answer
558.9k+ views
Hint:In the above question, is based on the concept of trigonometry. The sine, cosine, tangent functions can be solved by solving the relationship between angles and sides of the triangle.
Using \[\dfrac{\pi }{4}\] as the angle we can find the length of sides to get the value of each function.
Complete step by step solution:
Given is the angle which is \[\dfrac{\pi }{4}\] or \[{45^ \circ }\].So to solve the value of functions, we
need to know that one angle in the triangle is always \[{90^ \circ }\].Since we want to find the function for the angle for \[{45^ \circ }\],so the other angle in the triangle is \[{45^ \circ }\].
The total angle of triangle is \[{180^ \circ }\].Therefore by adding two angles and subtracting it with
\[{180^ \circ }\] we get a third angle.
\[{180^ \circ } - ({90^ \circ } + {45^ \circ }) = {45^ \circ }\].
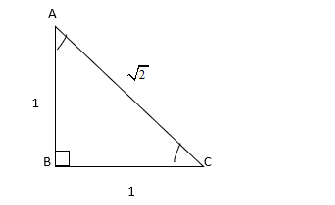
So, we consider the unit triangle \[\vartriangle ABC\]where two sides are equal. Since the two sides of triangles are equal, the triangle is an isosceles triangle. Therefore, by applying Pythagoras theorem, we
get \[AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \]
Now, we have to apply the trigonometric properties for different functions. For sine function the formula is the opposite side divided by hypotenuse.
\[\sin {45^ \circ } = \dfrac{1}{{\sqrt 2 }}\]
For cosine function, the formula is adjacent side divided by hypotenuse. Therefore, we get
\[\cos {45^ \circ } = \dfrac{1}{{\sqrt 2 }}\]
For tangent function, the formula is sine function divided by cosine function. \[\]
\[\tan {45^ \circ } = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{{\sqrt 2 }}}} = 1\]
Therefore, we get the above values.
Note: An important thing to note is that \[\dfrac{1}{{\sqrt 2 }}\] can also be further solved to get a decimal numbers.So, rationalizing it with \[\sqrt 2 \],we get \[\dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}\].The value of \[\sqrt 2 \]is 1.414,therefore dividing it by 2 we get
0.707.
Using \[\dfrac{\pi }{4}\] as the angle we can find the length of sides to get the value of each function.
Complete step by step solution:
Given is the angle which is \[\dfrac{\pi }{4}\] or \[{45^ \circ }\].So to solve the value of functions, we
need to know that one angle in the triangle is always \[{90^ \circ }\].Since we want to find the function for the angle for \[{45^ \circ }\],so the other angle in the triangle is \[{45^ \circ }\].
The total angle of triangle is \[{180^ \circ }\].Therefore by adding two angles and subtracting it with
\[{180^ \circ }\] we get a third angle.
\[{180^ \circ } - ({90^ \circ } + {45^ \circ }) = {45^ \circ }\].
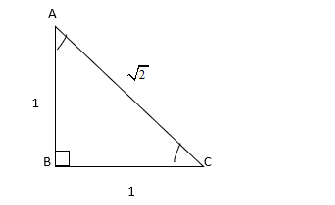
So, we consider the unit triangle \[\vartriangle ABC\]where two sides are equal. Since the two sides of triangles are equal, the triangle is an isosceles triangle. Therefore, by applying Pythagoras theorem, we
get \[AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \]
Now, we have to apply the trigonometric properties for different functions. For sine function the formula is the opposite side divided by hypotenuse.
\[\sin {45^ \circ } = \dfrac{1}{{\sqrt 2 }}\]
For cosine function, the formula is adjacent side divided by hypotenuse. Therefore, we get
\[\cos {45^ \circ } = \dfrac{1}{{\sqrt 2 }}\]
For tangent function, the formula is sine function divided by cosine function. \[\]
\[\tan {45^ \circ } = \dfrac{{\dfrac{1}{{\sqrt 2 }}}}{{\dfrac{1}{{\sqrt 2 }}}} = 1\]
Therefore, we get the above values.
Note: An important thing to note is that \[\dfrac{1}{{\sqrt 2 }}\] can also be further solved to get a decimal numbers.So, rationalizing it with \[\sqrt 2 \],we get \[\dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}\].The value of \[\sqrt 2 \]is 1.414,therefore dividing it by 2 we get
0.707.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a labelled diagram of the human heart and label class 11 biology CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE




