Question

How do you evaluate ${\sin ^{ - 1}}\left( 0 \right)$?

Answer 1

Hint: The arcsine is used to represent the inverse trigonometric function sine. The range of arcsine is from negative $\dfrac{\pi }{2}$ to positive $\dfrac{\pi }{2}$ and the domain of arcsine is from negative $1$ to positive $1$. It is a bijective function which means that it will be invertible. Using this property will be very useful for solving the given question.

Complete step by step solution:
Given is ${\sin ^{ - 1}}\left( 0 \right)$.
We have to find the value of ${\sin ^{ - 1}}\left( 0 \right)$.
Before starting solving the question, let us first draw a triangle with $\sin x = 0$.
In the given right-angled triangle,

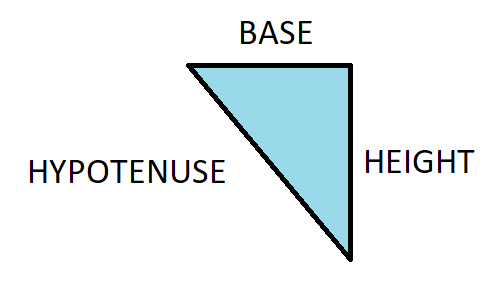
We consider the angle between base and hypotenuse as $x$. The angle between the base and perpendicular (also called as height) is ${90^ \circ }$. Now, let us take sine function on both the sides and we get,
$\sin \left( {{{\sin }^{ - 1}}\left( 0 \right)} \right) = \sin \left( x \right)$
As we already know the trigonometric property i.e., $\sin \left( {{{\sin }^{ - 1}}\theta } \right) = \theta $, so in the above equation we have, $\theta = 0$.
So, now the equation changes to $\sin \left( x \right) = 0$.
We know that the value of $\sin \theta $ varies for different values of $\theta $, so
$x = 0 + k\pi $, because $\sin k\pi = 0$ and where $k$ is any integer.

Hence, our answer is $x = k\pi $, where $k$ is any integer.

Note: The arcsin is the inverse of the trigonometric function sine. It is also a bijective function, which means that it gives a unique value of every unique input and for every output one single input is taken into consideration. Being a bijective function, also means that it is invertible, that’s why we were able to change arcsine to sine so easily. This specific property is valid only for its respective domain, that is from a negative one to a positive one.