Question

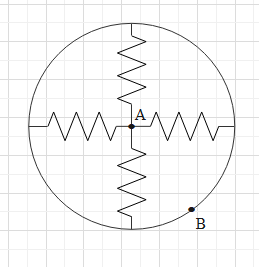
What is the equivalent resistance if the network between points A and B. (All the resistances are equal to r)

Answer 1

Hint: Find the current in of the resistance when a cell of emf V is connected arcos the points A and B. Let point A be at a higher potential than the potential at point B. then find the current in each of the resistance using Ohm’s law. Later find the total current. With this find the equivalent resistance.

Formula used:
$V = iR$

Complete step-by-step answer:
Suppose we connect a cell of emf V across the points A and B. Let the positive terminal (terminal with higher potential) of the cell be connected to point A and the negative terminal (terminal with lower potential) of the cell be connected to point B.
Therefore, a potential difference will be produced across the points A and B, which will be equal to V. Let us assume that the potential at point B be 0V and the potential at point A be at V.
Therefore, the ends of the resistors attached to A will be at potential V and other ends will be at 0V potential. This means the potential difference across all the resistances is V.
From Ohm’s law, we know that V = iR, where i is the current in the resistance R.
Therefore, the current in each of the resistances is $i=\dfrac{V}{r}$.
This means the total current in the circuit is $i+i+i+i=4i$.
Now, equivalent resistance is that resistance which when connected between the same potential difference (i.e. V), yields the same current as in the above circuit (i.e. 4i).
Let the equivalent resistance be ${{R}_{eq}}$.
$\Rightarrow V=4i{{R}_{eq}}$ ….. (i)
But, we know that $i=\dfrac{V}{r}$.
Substitute the value of i in (i).
 $\Rightarrow V=4\left( \dfrac{V}{r} \right){{R}_{eq}}$
$\Rightarrow {{R}_{eq}}=\dfrac{r}{4}$.
Hence, the equivalent resistance across points A and B is $\dfrac{r}{4}$.

Note: Since the four resistance have the same potential difference across them, they are in parallel connection.
When resistances are in parallel connection, the reciprocal of the equivalent resistance is equal to the sum of the reciprocals of the individual resistances.
i.e. $\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+......+\dfrac{1}{{{R}_{n}}}$ (when n resistances are in parallel connection).
Therefore, in the case we get
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{r}+\dfrac{1}{r}+\dfrac{1}{r}+\dfrac{1}{r}=\dfrac{4}{r}$
$\Rightarrow {{R}_{eq}}=\dfrac{r}{4}$