Question

What is the equation of the line perpendicular to $3x+4y=12$ and goes through (7,1)?

Answer 1

Hint: We need to study the slope intercept form of the line equation and then using the slope and some properties of the perpendicular lines will give us the required result. Apart from this we majorly need to use reciprocal property of slopes for perpendicular lines.

Complete step by step solution:
Now we need to transform the standard form equation $3x+4y=12$ into a slope intercept form equation $(y=mx+b)$ to find the slope of the line.
$3x+4y=12$ (now subtracting 3x on both sides we get)
$4y=12-3x$ (now divide both sides by 4 we will get)
$y=\dfrac{12}{4}-\dfrac{3}{4}x$
$y=-\dfrac{3}{4}x+3$
So now the slope of our first line is $-\dfrac{3}{4}$ and we know that perpendicular lines have reciprocal slopes, so if the slope of one is x, then the slope of other one is$\dfrac{1}{x}$ as we know that product of slopes of two perpendicular lines is -1.
For our question the slope of one line is $-\dfrac{3}{4}$ so the slope of the other line is reciprocal of this which is $\dfrac{4}{3}$ . Now we have the condition that we need to find the equation of the line such that it passes through the point (7,1), so for that we need to substitute the value of this point in the equation of the required line which is $y=\dfrac{4}{3}x+b$ and y=1 and x=7 so for value of b we have $1=\dfrac{4}{3}\times 7+b$
And further solving this we get
$\begin{align}
  & \Rightarrow b=1-\dfrac{28}{3} \\
 & \Rightarrow b=-\dfrac{25}{3} \\
\end{align}$
Therefore, the equation of the line is $y=\dfrac{4}{3}x-\dfrac{25}{3}$ or $4x-3y=25$.

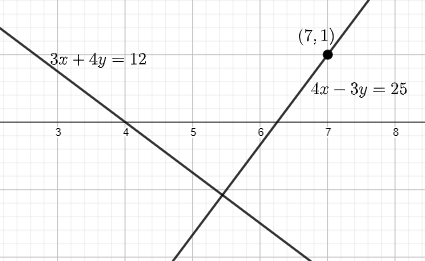
Note: We must know the various forms of equations of line and use accordingly. Slope intercept concept is important and is used in various such questions. We can try to remove the fractions from the equations as it reduces the chances of error.