Question

Equal masses of three liquids are kept in three identical cylindrical vessels A, B and C. There densities are\[{{\rho }_{A}},{{\rho }_{B}}\text{ and }{{\rho }_{C}}\] with \[{{\rho }_{A}}<{{\rho }_{B}}<{{\rho }_{C}}\]. The force on the base will be –
A) Maximum in vessel A.
B) Maximum in vessel B.
C) Maximum in vessel C.
D) Same in all the vessels.

Answer 1

Hint: We need to understand the relation between the densities of the three liquids and the force acting on the base of the cylinder. The pressure applied by the liquids in the identical cylinders need to be taken into consideration for solving.

Complete answer:
We are given three identical cylindrical vessels. It is said that each of them is filled with a liquid. All the three liquids are different and are named as A, B and C. It is also given that they have the densities \[{{\rho }_{A}},{{\rho }_{B}}\text{ and }{{\rho }_{C}}\] which are related as \[{{\rho }_{A}}<{{\rho }_{B}}<{{\rho }_{C}}\]. Also, the important point to be noted is that the equal mass of each liquid is filled in each of the cylinders.
Now, let us consider the pressure acting at a height ‘h’ from the base of each cylindrical vessel. We know that this hydrostatic pressure can be given as –
\[P=\rho gh\]
We know that the force acting on the base of the cylinder due to the pressure can be given by finding the product of the pressure and the base area ‘A” as –
\[\begin{align}
  & F=PA \\
 & \Rightarrow F=\rho gh.A \\
\end{align}\]
Now, we can see from the above relation that the density and the volume occupied by the liquid is dependent on the force acting on the base of the vessel. We already know that the mass of each of the given liquids is the same. So, the product of the density and the volume in the above formula remains constant for all the liquids as it accounts for the mass of the liquid as –
\[m=\rho hA\]
We can understand that for the three liquids with different densities occupying a vessel of equal base area will have different heights as shown below. i.e., the heights will be \[{{h}_{A}}>{{h}_{B}}>{{h}_{C}}\].
    

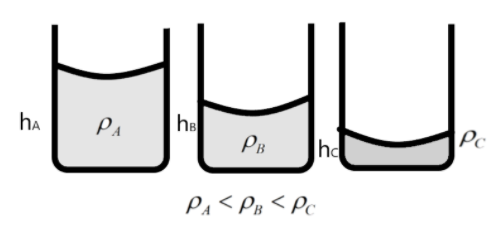
So, we can give the forces of each of the base of the cylindrical vessel as –
\[\begin{align}
  & {{\rho }_{A}}{{h}_{A}}A={{\rho }_{B}}{{h}_{B}}A={{\rho }_{C}}{{h}_{C}}A \\
 & \text{Also,} \\
 & {{m}_{A}}={{m}_{B}}={{m}_{C}} \\
 & \Rightarrow {{F}_{A}}={{m}_{A}}g=mg \\
 & \Rightarrow {{F}_{B}}={{m}_{B}}g=mg \\
 & \Rightarrow {{F}_{C}}={{m}_{C}}g=mg \\
 & \therefore {{F}_{A}}={{F}_{B}}={{F}_{C}} \\
\end{align}\]
Thus, we can see that the force acting on each of the cylinders is the same.

The correct answer is option D.

Note:
The force acting on the base of an open vessel with any liquids will be the same with the same mass. If the masses are also different, then this condition will not be applicable as the product of volume and density will not be the same in such a condition.