Question

EMF of the Daniell cell was found using different concentrations of \[Z{n^{2 + }}\] ion and \[C{u^{2 + }}\] ion. A graph was then plotted between \[{E_{cell}}\] and \[\log \dfrac{{[Z{n^{2 + }}]}}{{[C{u^{2 + }}]}}\] . The plot was found to be linear with intercept on. \[{E_{cell}}\] axis equal to \[1.10{\text{ }}V\] . Calculate \[{E_{cell}}\] for \[Zn\mid Z{n^{2 + }}(0.1M)\mid \mid C{u^{2 + }}(0.01M)\mid Cu\].

Answer 1

Hint:The electrode potential is denoted as \[(E)\] . The electrode potential defines the equilibrium potential difference between the metal electrode and the solution surrounding it. It can also be defined as the tendency of an electrode to lose or gain electrons. In an electrode potential if oxidation takes place it is called oxidation potential. Whereas, in an electrode potential if reduction is taking place then it is termed as reduction potential. In oxidation potential, the electrode loses its electron and in reduction potential, the electrode gains the electrons.

Complete step-by-step answer:By the Nernst equation;
\[{E_{cell}}\, = \,E_{cell}^0\, - \,\dfrac{{0.0591}}{n}\,\log \dfrac{{[oxidised]}}{{[reduced]}}\]
We know that for the linear equation is;
\[y\, = \,c\, + \,mx\]
Therefore, \[y\] will be \[{E_{cell}}\] , \[c\] will be \[E_{cell}^0\] and the remaining term \[mx\] will be \[\, - \,\dfrac{{0.0591}}{n}\,\log \dfrac{{[Z{n^{2 + }}]}}{{[C{u^{2 + }}]}}\] where \[x\] will be \[\log \dfrac{{[Z{n^{2 + }}]}}{{[C{u^{2 + }}]}}\].

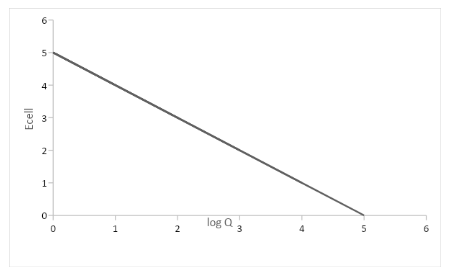
In this graph, we are able to observe that \[log{\text{ Q}}\] is \[\log \dfrac{{[Z{n^{2 + }}]}}{{[C{u^{2 + }}]}}\] which is on \[x\] axis and \[{E_{cell}}\] vales on \[y\] axis.
Where the given intercept value which will be our term \[c\] .
\[E_{cell}^0\, = \,1.10\,V\]
Now, we need to find \[{E_{cell}}\].
So, let’s write the reaction in which the values are given;
\[Zn\mid Z{n^{2 + }}(0.1M)\mid \mid C{u^{2 + }}(0.01M)\mid Cu\]
\[Zn\, + \,C{u^{2 + }}\, \to \,Z{n^{2 + }}\, + \,Cu\,\]
In the reaction, we are able to observe that \[Zn\] is getting oxidized to form \[Z{n^{2 + }}\] where the reaction is taking place at anode electrode. On the other hand, \[C{u^{2 + }}\] is getting reduced to form \[Cu\,\] at cathode electrodes.
By the reaction we are able to observe that the number of transfer electrons are \[2\] . \[\]
Therefore, \[n\, = \,2\]
\[{E_{cell}}\, = \,E_{cell}^0\, - \,\dfrac{{0.0591}}{2}\,\log \dfrac{{[Z{n^{2 + }}]}}{{[C{u^{2 + }}]}}\]
Now, we know that the given values for each is;
\[E_{cell}^0\, = \,1.10\,V\]
\[n\, = \,2\]
\[Z{n^{2 + }}\, = \,0.1M\]
\[C{u^{2 + }}\, = \,0.01M\]
Let’s substitute the value in the above equation.
We get;
\[{E_{cell}}\, = \,E_{cell}^0\, - \,\dfrac{{0.0591}}{2}\,\log \dfrac{{[0.1]}}{{[0.01]}}\]
\[{E_{cell}}\, = \,E_{cell}^0\, - \,\dfrac{{0.0591}}{2}\,\log \,[10]\]
\[{E_{cell}}\, = \,E_{cell}^0\, - \,\dfrac{{0.0591}}{2}\, \times \,1\]
\[ = \,1.10\, - \,0.0295\]
\[ = \,1.0705\,V\]
Now we get the \[{E_{cell}}\] value where it is \[1.0705\,V\]

Note:The standard electrode potential which is denoted as \[({E^\circ })\] is a measurement of the potential for equilibrium. When there is a potential difference between the electrode and the electrolyte, then it is known as the potential of the electrode. And when unity is the concentration of all the species involved in a semi-cell, then the electrode potential is called the standard electrode potential.
The standard electrode potential is calculated by using the equation;
\[{E^\circ }_{cell}\, = \,{E^\circ }_{cathode}\, - \,{E^\circ }_{anode}\]