Question

Electrostatic potential at H is
A. \[\dfrac{\sigma }{{^{{\varepsilon _0}}}}\left[ {{{\left( {{a^2} - {H^2}} \right)}^{1/2}} - H} \right]\]
B. \[\dfrac{\sigma }{{^{{\varepsilon _0}}}}\left[ {{{\left( {{a^2} - {H^2}} \right)}^{1/2}} + H} \right]\]
C. \[\dfrac{\sigma }{{^{2{\varepsilon _0}}}}\left[ {{{\left( {{a^2} + {H^2}} \right)}^{1/2}} - H} \right]\]
D. \[\dfrac{\sigma }{{^{2{\varepsilon _0}}}}\left[ {{{\left( {{a^2} - {H^2}} \right)}^{1/2}} - H} \right]\]

Answer 1

Hint:In this question,we are going to use the concept of electrostatic potential and derive the expression of it by assuming certain assumptions.The
potential due to point charge is inversely proportional to square root of distance.

Complete step by step answer:
 First let’s calculate potential due to a ring on a point lying on its axis, then we will use it to calculate potential due to disc.

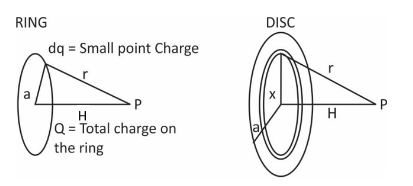
Consider a small point charge on the ring having small charge dq. Now potential due to this point charge can be written as
\[dv = \dfrac{{K(dq)}}{{{r^2}}}\]
Total potential due to ring: \[V = \int {dv} \]
\[V = \int {\dfrac{{K(dq)}}{{{r^2}}}} \]
\[r = \sqrt {{H^2} + {a^2}} \]
\[V = \int {\dfrac{{K(dq)}}{{\sqrt {{H^2} + {a^2}} }}} \]
\[V = \dfrac{K}{{\sqrt {{H^2} + {a^2}} }}\int {dq} \]
\[V = \dfrac{{KQ}}{{\sqrt {{H^2} + {a^2}} }}\]
Now, Consider a small ring in a thin disc, the small ring has radius \[ = x\]and thickness\[ = dx\]. As we have already calculated the potential due to ring, we can say that potential due to the small ring is
\[dV = \dfrac{{Kdq}}{{\sqrt {{H^2} + {x^2}} }}\]
Now, we can integrate thin disc to get potential of entire disc
\[V = \int {dV} \]
\[V = \int {\dfrac{{Kdq}}{{\sqrt {{H^2} + {x^2}} }}} \]
Now we have to substitute dq charge in small ring to thickness dx in terms of x,
\[dq = \,\,\dfrac{{Total\,\,\,ch\arg e}}{{Total\,\,\,area}} \times Area\,\,\,of\,small\,\,ring\]
\[dq = \dfrac{Q}{{\pi {a^2}}} \times \left( {2\pi x} \right) \times dx\]
Area of ring is calculated by approximating small ring as rectangle of length equal to circumference of small ring and height equal to the thickness
\[V = \int {\dfrac{{KQ\,\,\,2\pi x}}{{(\pi {a^2})\,(\sqrt {{H^2} + {x^2}} )}}} dx\]
\[V = \dfrac{{KQ}}{{{a^2}}}\int {\dfrac{{2xdx}}{{\sqrt {{H^2} + {x^2}} }}} \]
Here the limit of $x$ is from $0$ to $a$
So, \[V = \dfrac{{KQ}}{{{a^2}}}\int_0^a {\dfrac{{2xdx}}{{\sqrt {{H^2} + {x^2}} }}} \] ….. (i)
Now, Substituting${H^2} + {x^2} = t$, putting for lower limit $x = 0$then ${H^2} + {0^2} = t$ $ \Rightarrow t = {H^2}$ now for upper limit $x = a$ then ${H^2} + {a^2} = t$,
${H^2} + {x^2} = t$
Differentiating, $t$ with respect to $x$ so, $2x{\text{ }}dx = dt$
Putting all above values in equation (i).
$V = \dfrac{{KQ}}{{{a^2}}}\int_{{H^2}}^{{H^2} + {a^2}} {\dfrac{{dt}}{{\sqrt t }}} $
$
V = \dfrac{{KQ}}{{{a^2}}}2\left( {\sqrt {{H^2} + {a^2}} - \sqrt {{H^2}} } \right) \\
V = \dfrac{{KQ}}{{{a^2}}}2\left( {\sqrt {{H^2} + {a^2}} - H} \right) \\
 $
Putting $K = \dfrac{1}{{4\pi {\varepsilon _0}}}$ and $\sigma = \dfrac{Q}{{\pi {a^2}}}$, we get
$V = \dfrac{\sigma }{{2\varepsilon o}}\left( {\sqrt {{H^2} + {a^2}} - H} \right)$
Here option (C) is the correct option.

Note:As the limits of $x$is from $0$to $a$and ${H^2} + {x^2} = t$
at $x = 0,{\text{ t}} = {H^2}$
at $x = a,{\text{ t}} = {{\text{H}}^2} + {a^2}$
So, the limits of $t$will be from ${H^2}$to ${H^2} + {a^2}$