Question

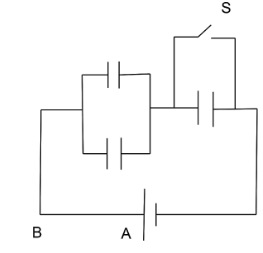
Each capacitor shown in figure has a capacitance of \[5.0\mu F\] . The emf of the battery is \[50V\]. How much charge will flow through AB if the switch S is closed?

Answer 1

Hint: the value of the capacitor connected to a switch will differ in the switched on and off conditions. When the switch is in the on state, the capacitor is assumed to be short but the charge is stored in it and doesn’t flow because it is considered short.

Formulas used:
\[{C_{parallel}} = {C_1} + {C_2}\]
\[\Rightarrow {C_{series}} = \dfrac{{{C_1} \times {C_2}}}{{{C_1} + {C_2}}}\]
\[\Rightarrow Q = CV\]
Total charge= total charge when switch closed – total charge when switch open

Complete step by step answer:
The following data is given in the question: voltage, \[V = 50V\].
Capacitance of each capacitor is \[C = 5.0\mu F\]
When $S$ is open the capacitors in parallel produce a value of \[10\mu F\].
The \[10\mu F\] capacitor is in series with the next \[5\mu F\] capacitor.
The total value of capacitance is \[\dfrac{{10 \times 5}}{{10 + 5}} = \dfrac{{50}}{{15}}= \dfrac{{10}}{3}\mu F\].
The total charge can be found using the formula:
\[Q = CV \\
\Rightarrow Q= \dfrac{{10}}{3} \times 50\,V \\
\Rightarrow Q= \dfrac{{500}}{3}\mu C\]

When the switch S is closed the capacitor connected to it gets cancelled and the equivalent value of capacitance will be the value of the other two: \[10\mu F\].Now the charge flowing will be \[Q = CV = 10 \times 50V = 500\mu C\]. Since the third capacitor is short there will be some amount of charge in that capacitor, making the total charge present to be:
\[500\mu C - \dfrac{{500}}{3}\mu C = \dfrac{{1500 - 500}}{3} \\
\Rightarrow 500\mu C - \dfrac{{500}}{3}\mu C = 333.3\mu C \\
\therefore 500\mu C - \dfrac{{500}}{3}\mu C = 3.34 \times {10^{ - 4}}C\]

Hence, the total charge flowing through AB when the switch is on is \[3.34 \times {10^{ - 4}}C\].

Note: One has to be clear with the switch open and switch closed condition and how current passes through it to attempt this question. The function of the capacitor connected to the switch when turned on is also crucial. The calculation of capacitance in series and parallel need to be checked twice as we might have the tendency to use the formula of resistors.