Question

$E$ and $F$ are the points on the sides $PQ$ and $PR$ of a$\Delta PQR$. For each of the following cases state whether \[EF\parallel QR\]:
A) $PE = 3.9cm$, $EQ = 3cm$,$PF = 3.6cm$,$FR = 2.4cm$
B) $PE = 4cm$, $QE = 4.5cm$,$PF = 8cm$, $RF = 9cm$
C) $PQ = 1.28cm$, $PR = 2.56cm$,$PE = 0.18cm$, $PF = 0.36cm$

Answer 1

Hint:
A) In order to prove \[EF\parallel QR\], we have to prove that $\dfrac{{PE}}{{EQ}} = \dfrac{{PF}}{{FR}}$ because according to converse of basic proportionality theorem, if a line divides any two sides of the triangle in the same ratio then that line is parallel to the third side of the triangle.
B) In order to prove \[EF\parallel QR\], we have to prove that $\dfrac{{PE}}{{EQ}} = \dfrac{{PF}}{{FR}}$ because according to converse of basic proportionality theorem if a line divides any two sides of the triangle in the same ratio then that line is parallel to the third side of the triangle
C) In order to prove \[EF\parallel QR\], we have to prove that $\dfrac{{PE}}{{EQ}} = \dfrac{{PF}}{{FR}}$ because according to converse of basic proportionality theorem if a line divides any two sides of the triangle in the same ratio then that line is parallel to the third side of the triangle

Complete step-by-step answer:
A) $\left( 1 \right)$ In the given data, $PE = 3.9cm,EQ = 3cm,PF = 3.6cm,FR = 2.4cm$

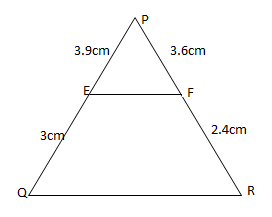
So, we can find $\dfrac{{PE}}{{EQ}} = \dfrac{{3.9}}{3}$
$\dfrac{{PE}}{{EQ}} = \dfrac{{39}}{{30}}$
$\dfrac{{PE}}{{EQ}} = \dfrac{{13}}{{10}}$
Also we can find $\dfrac{{PF}}{{FR}} = \dfrac{{3.6}}{{2.4}}$
$\dfrac{{PF}}{{FR}} = \dfrac{{36}}{{24}}$
$\dfrac{{PF}}{{FR}} = \dfrac{3}{2}$
Thus, $\dfrac{{PE}}{{EQ}} \ne \dfrac{{PF}}{{FR}}$
Therefore, $EF{\text{ and QF}}$ are not parallel.
B)

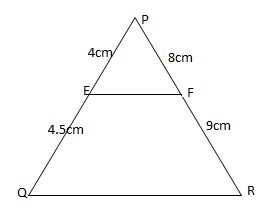
In the given data it is mentioned that $PE = 4cm$, $QE = 4.5cm$, $PF = 8cm$, $RF = 9cm$
So, we can find $\dfrac{{PE}}{{EQ}} = \dfrac{4}{{4.5}}$
$\dfrac{{PE}}{{EQ}} = \dfrac{{40}}{{45}}$
$\dfrac{{PE}}{{EQ}} = \dfrac{8}{9}$
Also we can find $\dfrac{{PF}}{{FR}} = \dfrac{8}{9}$
Since both of them equals to $\dfrac{8}{9}$
Therefore, $\dfrac{{PE}}{{EQ}} = \dfrac{{PF}}{{FR}}$
Thus, it is proved that $EF$ and $QR$ are parallel.
C)

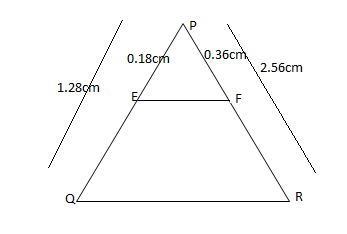
It is given data, $PQ = 1.28cm$, $PR = 2.56cm$,$PE = 0.18cm$, $PF = 0.36cm$
It is clear from the diagram that $PQ = PE + EQ$
Here we have to find,
$EQ = PQ - PE$
$ = 1.20 - 0.18$
$ = 0.10$
In the similar way $PR = PF + FR$
We have to find
$FR = PR - PF$
$ = 2.56 - 0.36$
$ = 2.20$
Therefore, $\dfrac{{PE}}{{EQ}} = \dfrac{{0.18}}{{1.10}}$
 $\dfrac{{PE}}{{EQ}} = \dfrac{{18}}{{110}}$
 $\dfrac{{PE}}{{EQ}} = \dfrac{9}{{55}}$
Also, $\dfrac{{PE}}{{FR}} = \dfrac{{0.36}}{{2.2}}$
$\dfrac{{PE}}{{FR}} = \dfrac{{36}}{{220}}$
$\dfrac{{PE}}{{FR}} = \dfrac{{18}}{{110}}$
$\dfrac{{PE}}{{FR}} = \dfrac{9}{{55}}$
 As both are equals to $\dfrac{9}{{55}}$
Therefore, $\dfrac{{PE}}{{EQ}} = \dfrac{{PF}}{{FR}}$
Hence both of them are parallel.

Note: Triangle can be defined as a two dimensional figure with three sides and three vertices.
Converse of basic proportionality theorem states that if lines divide any of the two sides of a triangle in the same ratio, then that line must be parallel to the third side.
Length of the third side of the triangle is always smaller than the sum of other sides of the triangle.
Triangles are classified on the basis of angle and length. In case of classification according to length of sides it is of three types like scalene triangle, Isosceles triangle and equilateral triangle. On the basis of angle there are three types of triangle like right angled triangle, obtuse angled triangle and acute angled triangle.