Question

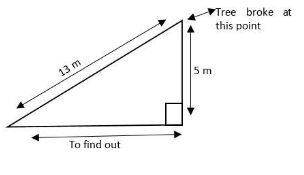
Due to strong wind, a part of a tree 18 m high broke at a distance of $ 5\,m $ from the ground, without separating from the main stem, the top of the tree touched the ground. At what distance from the foot of the step did the top of the tree fall on the ground?

Answer 1

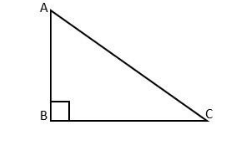
Hint: : In a right-angled triangle [i.e. triangle in which one of the angle is 90˚], Pythagora's theorem can be applied. Here, triangle ABC is right-angled of vertex B. $ \angle ABC = \dfrac{\pi }{2} = 90^\circ $
Pythagoras theorem,
It states that in a right-angled triangle,
 $ {(Base)^2} + {(perpendicular)^2} = {(Hypotenuse)^2} $
i.e.
Square of length of base plus square of length of perpendicular is equal to square of length of Hypotenuse.
Here, in right-angled triangle ABC:
AB is perpendicular
BC is Base
AC is Hypotenuse.
 $ \Rightarrow $ Length of Base $ = $ BC
Length of perpendicular $ = $ AB
Length of Hypotenuse $ = $ AC
So,
According to Pythagoras theorem,
 $ {(BC)^2} + {(AB)^2} = {(AC)^2} $

Complete step-by-step answer:

Here, in our question,
Length of tree $ 18\,m $
After braking,
Length of part of tree from ground $ = 5\,m $
Length of part of tree which brake and touched the ground $ = 18\,m - 5\,m $
 $ = 13\,m. $
So, we have to find out the distance from the foot of the step did the top of the tree fall on the ground:
So, Here Right-angled triangle is formed. Applying Pythagoras theorem,
\[
  {(AB)^2} + {(AC)^2} = {(BC)^2} \\
   \Rightarrow {(5)^2} + {(AC)^2} = {(13)^2} \\
   \Rightarrow {(AC)^2} = {(13)^2} - {(5)^2} \\
   \Rightarrow AC = \sqrt {169 - 25} = \sqrt {144} = 12\,m \\
 \] $
  AB \to perpendicular \\
  AC \to Base \\
  BC \to Hypotenuse \\
  $
Hence,
The required answer is $ 12\,m. $

Note: The most important thing in this situation is deciding the length of hypotenuse that is part of the tree fell due to wind, one may tend to take it as 18m but since tree fell from the distance of 5m , the remaining 13m will be on the ground.This is very crucial to identify.