Question

$ DUCK $ is a parallelogram and $ O $ is the point of intersection of the diagonals. If $ OC = 4{\rm{ cm}} $ and $ UK $ is $ 4{\rm{ cm}} $ more than $ DC $ find $ OK $ .

Answer 1

Hint: Since, $ O $ is the midpoint of the diagonal, and since $ OC $ is known then the $ DC $ will be equal to twice of $ OC $ . Since $ DC $ is found and $ UK $ is four more than $ DC $ . Hence $ UK $ is found. And it is known that $ O $ divides the diagonal into two equal parts. So $ OK $ will be equal to half of $ UK $ .

Complete step-by-step answer:
Given:
It is given that $ DUCK $ is a parallelogram.
And where $ DC $ and $ UK $ are diagonals.
Given that the length of $ OC = 4{\rm{ cm}} $ .
The following is the schematic diagram of the parallelogram DUCK.

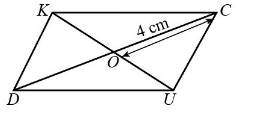
From the diagram, we get the point at which diagonals intersect is $ O $ . Hence $ O $ is the midpoint of diagonals.
The main aim is to find the length of $ OK $ .
It is given that the length of $ OC $ is $ 4{\rm{ cm}} $ . Since, $ O $ divides the diagonal into two equal parts , so $ DC $ is equal to twice the length of $ OC $ .
 $ \begin{array}{c}
DC = 2 \times OC\\
 = 2 \times 4{\rm{ cm}}\\
 = 8{\rm{ cm}}
\end{array} $
Hence, the length of one diagonal $ DC $ is $ 8{\rm{ cm}} $ .
It is given that the length of $ UK $ is $ 4{\rm{ cm}} $ more than $ DC $ , then we can say that,
  $ \begin{array}{c}
UK = 4 + DC\\
 = 4{\rm{ cm}} + 8{\rm{ cm}}\\
{\rm{ = 12 cm}}
\end{array} $
Since, the $ O $ divides diagonals into two equal parts, so $ OK $ is equal to half of the length of $ UK $ .
 $ \begin{array}{c}
OK = \dfrac{{UK}}{2}\\
 = \dfrac{{12}}{2}\\
 = 6{\rm{ cm}}
\end{array} $
Hence the length of $ OK $ in the $ DUCK $ parallelogram is $ 6{\rm{ cm}} $ .

Note: Since the $ DUCK $ is parallelogram in which the opposite sides are equal and opposite angles are also equal. This problem can be done in different ways, that is, it is a known fact that diagonals bisect in parallelograms. So $ OC = OD $ is equal to $ 4{\rm{ cm}} $ . It is given that $ UK $ is four more than $ DC $ . Substitute it in the equation we get the required value of $ OK $ .