Question

Draw the square ABCD of area 9 square centimeters.

Answer 1

Hint: As the formula for finding the area of square is (s x s), that is \[{{\left( s \right)}^{2}}\]
Therefore, the side of this square will be equal to 3 centimeters because, (3 x 3) or \[{{\left( 3 \right)}^{2}}=9\] .

For making a right angle, we must first draw a semicircle, then where the semicircle cuts the line, we make another cut on the semicircle by putting the compass at the cut. Now we make two cuts by placing the compass at both the prior two cuts and then make a line which passes through the intersection.

Complete step-by-step answer:
For the first step, we need to draw a line measuring 3 centimeter.

Now, secondly, draw another line forming a right angle at point B, measuring 3 centimeters.

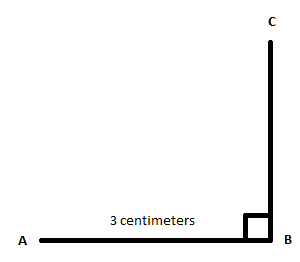
Thirdly, we need to draw one more line forming a right angle at point C, measuring 3 centimeters.

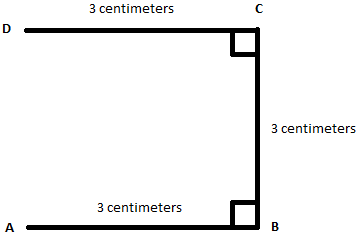
Lastly, we need to draw a line forming a right angle at point D, measuring 3 centimeters.

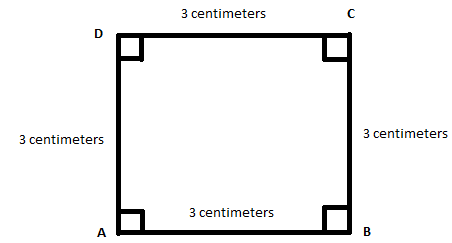
Now, let us calculate the area of this square ABCD,
Formula for the area of square = side x side
Area of the square ABCD = 3 x 3=9cm

Note:-
One must remember the formulas of the areas of some basic shapes such as rectangle, square, circle, triangle, rhombus, parallelogram, etc.
1. RECTANGLE: (l x b), i.e., (length x breadth), where length is the length of the rectangle and breadth is the breadth of the rectangle.

2. SQUARE: As mentioned above, (s x s) or \[{{\left( s \right)}^{2}}\], i.e., (side x side), where side refers to the length of one side of the square.

3. TRIANGLE - ( \[\dfrac{1}{2}base\times height\] ), where base refers to the length of the base of the triangle and height refers to the height of the triangle.

4. RHOMBUS - ( \[~\dfrac{1}{2}diagonal{{l}_{1}}\times diagonal{{l}_{2}}\] ), where diagonal₁ refers to the length of a diagonal of the rhombus and diagonals 2 refers to the length of other diagonal of the rhombus.

5. PARALLELOGRAM: (b x h), i.e., (base x height), where base refers to the length of the base and height refers to the height of the rhombus.

6. CIRCLE- \[(~\pi {{r}^{2}})\]where \[{{\left( radius \right)}^{2}}\] refers to the square of the length of the radius of the square.