Question

Draw the number line and represent the following rational number on it: \[\dfrac{{ - 7}}{4}\]

Answer 1

Hint: Here we look at the denominator of the number and figure out how many parts we need to divide the number line, and using the concept of fractions we plot the point on the number line. Observe the sign before the fraction and decide on which side of 0 the number lays on the number line.

Complete step-by-step solution:
We have to represent the point \[ - \dfrac{7}{4}\] on the number line.
Looking at the denominator of the fraction we can tell that the number of parts in which each part of the number line between two integers is divided.
Here the number in the denominator is 4. So, between every integer there are four parts.
Also, we calculate the value in decimal form which helps us to determine the range of the number line to be drawn.
Calculate the value of \[ - \dfrac{7}{4}\] by dividing numerator by denominator.
\[ \Rightarrow - \dfrac{7}{4} = - 1.75\]
Since the value of fraction is negative. We look at the left hand side of 0.
The number \[ - 2 < - 1.75 < - 1\]
We will divide the area between -1 and -2 in four parts and name the dividing line as the fraction. We increase the numerator by one numeric value as we move to the left hand side and keep the denominator fixed.
So, the first dividing line to left of 0 will be \[ - \dfrac{1}{4}\], second line to the left of 0 will be \[ - \dfrac{2}{4}\] and so on then the fourth dividing line to the left of 0 will be \[ - \dfrac{4}{4} = - 1\] which will become the integer -1 itself.
Then the first dividing line to left of -1 will be \[ - 1 + \left( { - \dfrac{1}{4}} \right) = - \dfrac{5}{4}\], second line to the left of -1 will be \[ - \dfrac{6}{4}\] and then the third dividing line to the left of -1 will be \[ - \dfrac{7}{4}\]
All values on the number line that are integers are always the fourth division line.
We plot all fractions in between -1 and -2 and represent the fraction \[ - \dfrac{7}{4}\] using different colors.

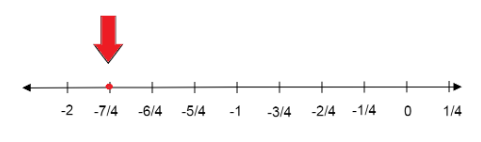
Thus, the representation of \[ - \dfrac{7}{4}\] on the number line is as above.

Note: Students should always first check the value of fraction and then plot it on the line. Many times students try to plot the fraction by representing the number line using decimals. In this case the division of numerator by denominator gives the value -1.75, so try to avoid plotting decimal points on the number line.