Question

Draw the graph of the equations $\,2x\,+\,3y\,=\,5\,$ and check whether the points (-3,4) and (1,-3) are solutions of the given equations.

Answer 1

Hint: Drawing an equation and checking the points.

Complete step by step solution:

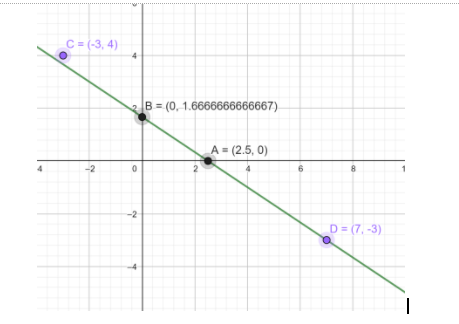
The straight line $\,2x\,+\,3y\,=\,5\,$ can be allotted in a graph by arranging it in a form of
\[\] \[y=mx+c\]. Where m is considered slope and c is considered y intercept.\[\]
After arranging $\,2x\,+\,3y\,=\,5\,$to \[y=-\dfrac{2}{3}x+\dfrac{5}{3}\] we get slope (\[m\]) as \[-\dfrac{2}{3}\]and y-intercept as \[-\dfrac{2}{3}\].
Thus, from the slope we conclude that the line is going downward (-ve slope means downward) , that is , it is decreasing. And the intercept shows that the line intercept at the y-axis at (0, 1.666667 ). [\[\dfrac{5}{3}\]=1.66667]
Now, to check whether the points (-3,4) and (7,-3) are solutions of this given line we need to put and of the points’ \[x\text{ }\!\!'\!\!\text{ s or }y's\]value in the equation.
Putting the value of \[x=-3\] from (-3,4) in the equation we get,
\[\begin{align}
  & y=-\dfrac{2}{3}\times (-3)+\dfrac{5}{3} \\
 & y=2+\dfrac{5}{3};\,\,\,\,\,\,\,\,\,\,\,y=\dfrac{6+5}{3}; \\
 & \therefore y=\dfrac{11}{3}\text{ which is not equal to y=4 from the points given to us}\text{.} \\
 & \therefore \text{(-3,4) is not a solution for this line}\text{.} \\
\end{align}\]
We again put,
\[\begin{align}
  & x=7\text{ from }(7,-3) \\
 & y=-\dfrac{2}{3}\times (7)+\dfrac{5}{3} \\
 & \therefore y=-\dfrac{14}{3}+\dfrac{5}{3}\,\,\,\,\,\,\,\,\,\,y=\dfrac{-14+5}{3} \\
 & \therefore y=\dfrac{-9}{3}=-3\text{ which is equal to }y=-3\text{ from the point (7,-3)} \\
 & \therefore \text{ (7,-3) is a solution for this line}\text{.} \\
\end{align}\]

Note: If a similar line or any straight line is given to us we first need to check its slope by comparing it to \[y=mx+c\]. After verifying if the line is going upward or downward according to the we will check the y-intercept. Suppose the y-intercept is 0, this means that the line passes from the origin (0,0). Accordingly, if we want to check whether the points given in the equations are lying on the straight line or not, we will have to put those points on the straight line equation. By putting the value of x from the points given to us, in the equation we will find the value of y. Now, if the value of y we found from the equation matches with the value given to us, then we can conclude that the point lies or the point is the solution for the equation.