Question

Draw the graph of the equation $x+3y=15$. Find the co-ordinates of the point where the graph intersects the $x$- axis.

Answer 1

Hint: In this question, we will use the line equation to draw the graph. First, we will consider $x=0$, and find $y$ by substituting in the line equation. Next, we will substitute $y=0$, and find $x$ by substituting in the line equation. Plot the obtained points in the graph and draw the line equation. In the end, the intersection of the line equation on the $x$- axis will give the co-ordinates.

Complete step-by-step answer:
Here, we have been given the equation $x+3y=15$ and we need to find the co-ordinates of the point where the line equation intersects the $x$- axis.
Let us first find the co-ordinates of the line equation $x+3y=15$.
For this, we need to consider $x=0$ and find the value of $y$, then consider $y=0$ and find the value of $x$. When you find the value of $x$, that is where the line equation drawn in the graph intersects the $x$- axis.
When, $x=0$,
Substitute $x=0$ in $x+3y=15$, we get
$0+3y=15$
Now, divide by 3 on both the sides of the equation, we get
$\begin{align}
  & \dfrac{3y}{3}=\dfrac{15}{3} \\
 & y=5
\end{align}$
Therefore, let us say A $\left( x,\,y \right)$ = A $\left( 0,\,\,5 \right)$.
When, $y=0$,
Substitute $y=0$ in $x+3y=15$, we get
$x+3\left( 0 \right)=15$
      $x+0=15$
             $x=15$
Therefore, let us consider B $\left( x,y \right)$ = B $\left( 15,\,0 \right)$.
Now, we have two points A (0, 5) and B (15, 0), we will plot the points on the graph and create the line.

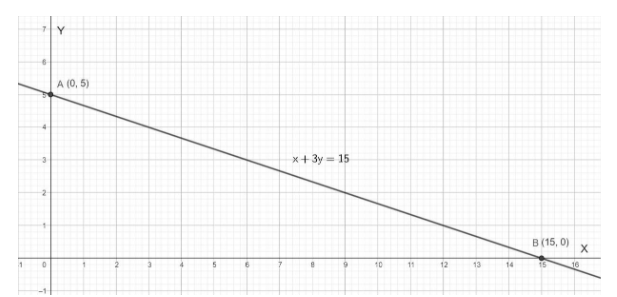
You can see from the graph, the line equation $x+3y=15$, intersects the \[x\]- axis at (15, 0).
Hence, the point where the line intersects the $x$- axis is (15, 0).

Note: Here, we also find the intersection point of the line equation and the $x$- axis by substituting $y=0$ in the line equation and we will get the co-ordinates of the intersection.