Question

Draw the graph of $\log x$ .

Answer 1

Hint: For answering this question we need to draw a graph for the function $\log x$ . For that we will plot a curve for the respective values of $x$ and explore the basic definition of $\log x$ . The basic definition of $\log x$ says that for ${{a}^{y}}=x$ the logarithm value is given as $y={{\log }_{a}}x$ .

Complete step-by-step answer:
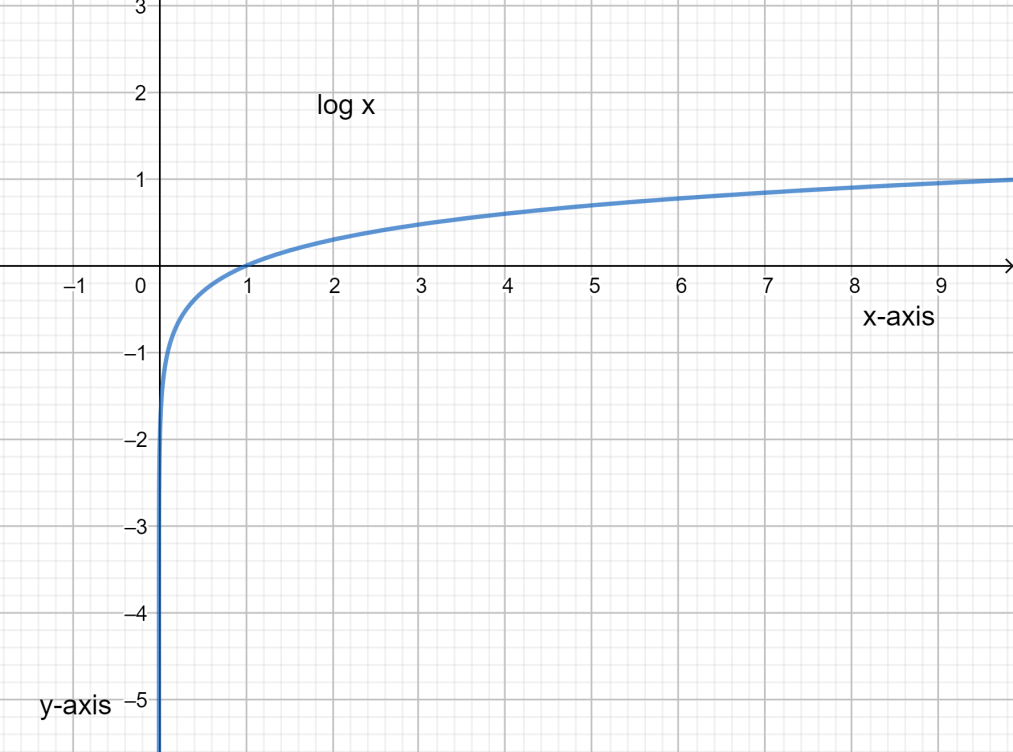
Now considering from the question we need to draw the graph for the function of $\log x$ .
From the basic definition of logarithm of a value for a function ${{a}^{y}}=x$ is given as $y={{\log }_{a}}x$ for $a > 0,a\ne 1$ . Here $x > 0$ is the domain for this function.
The graph will be continuous and smooth.
The curve is increasing for $a > 1$ and decreasing for $0 < a < 1$ .
The curve of $\log x$ intersects the x-axis when $x=1$ .
The logarithm function is of one-one type.
The logarithm function is the inverse of the exponential function.
Properties:

(i) ${{\log }_{a}}1=0$ because ${{a}^{0}}=1$ .
(ii) ${{\log }_{a}}~a\text{ }=\text{ }1$ because ${{a}^{1}}=a$ .
(iii) ${{\log }_{a}}{{a}^{x}}=x$ .
(iv) ${{\log }_{a}}x={{\log }_{a}}y\Rightarrow x=y$ .
(v) ${{\log }_{a}}x={{\log }_{b}}x\Rightarrow a=b$ .
Common logarithm has base 10 represented by $\log x$ .
Natural logarithm has a base $e$ represented by $\ln x$ .
Here we need to draw a graph of common logarithms.

Note: For answering questions based on logarithm functions we use different formulae like
$\log \left( ab \right)=\log a+\log b$, $\log \left( \dfrac{a}{b} \right)=\log a-\log b$ and many more. The logarithm properties give that $\ln e=1$ and $\log 10=1$ . There is also one special property given as ${{\log }_{a}}b=\dfrac{\log b}{\log a}$ and ${{\log }_{a}}b=\dfrac{1}{{{\log }_{b}}a}$ . As this is an inverse function we can say that ${{\log }_{a}}\left( {{x}^{n}} \right)=n{{\log }_{a}}x$ and ${{\log }_{a}}\left( \sqrt[n]{x} \right)=\dfrac{1}{n}{{\log }_{a}}x$ . We can say ${{a}^{{{\log }_{a}}x}}=x$ and ${{\log }_{a}}0=\left\{ \begin{matrix}
   -\infty \text{ when a > 1} \\
   \infty \text{ when a < 1} \\
\end{matrix} \right\}$ . We have another formulae saying that ${{\log }_{{{a}^{m}}}}{{a}^{n}}=\dfrac{n}{m}$ for $m\ne 0$ .