Question

Draw parallelogram ABCD with AC = 9 cm, BD = 7 cm and \[\angle AOB = 120^\circ \] where $\overline {AC} $ and $\overline {BD} $ intersect at O and find its area

Answer 1

Hint: In the given question, we have to draw a parallelogram whose diagonals are given and the angle between the two diagonals is given. We know that the diagonals of a parallelogram bisect each other, that is, they cut each other in equal halves at the point of intersection. So using this property, we have to first construct the two diagonals and join all the corner points to get the parallelogram.

Complete step-by-step answer:
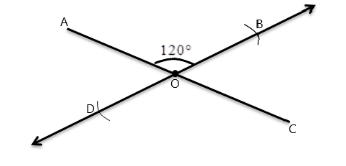
AC is a diagonal of length 9 cm, so we first draw a line segment of length 9 cm and mark the midpoint of this line segment.
 

Through the midpoint of AC draw another line segment such that the angle between AC and BD is $120^\circ $ , now from the point O, draw two arcs of length 3.5 cm on both the sides of the line segment.

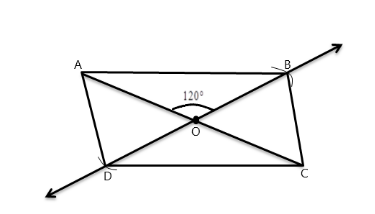
Join the points A, B, C and D to get the required parallelogram.

Now, drop a perpendicular from point B to side DC, to find the height of the parallelogram.

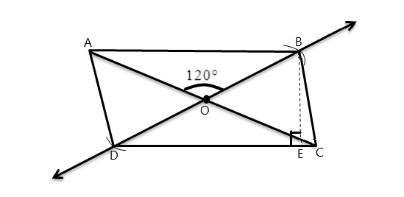
BD is the height of the parallelogram and CD is the base of the parallelogram, so measuring the length of BD and CD, we get –
 \[BE = h = 4\;cm\] and \[CD = b = 7{\text{ }}\;cm\]
Hence, the area of the parallelogram ABCD is,
$Area = base \times height = 7 \times 4 = 28\;c{m^2}$ .
So, the correct answer is “$28\;c{m^2}$”.

Note: A parallelogram is a quadrilateral that has four sides. Its opposite sides are equal and the opposite angles are also equal. The opposite sides of a parallelogram are equal. The region bounded by a parallelogram is called its area, but to find out the area, we have to first find out its height as the area is the product of the base and the height of the parallelogram.