Question

Draw circuit diagram of R-C phase-shift oscillator. Find frequency of oscillation if $R= 13k\Omega$ and $C=5 \mu F$.

Answer 1

Hint: RC circuit is a combination of an amplifier and RC feedback network. A typical R-C circuit has a combination of three resistors and capacitors. Use these details to draw the circuit diagram of R-C phase-shift oscillator. Then, to find the frequency of oscillation use the formula for frequency of R-C phase-shift oscillator. Substitute the given values and find the frequency of oscillation.
Formula used:
$f = \dfrac {1}{2 \pi RC \sqrt {2N}}$

Complete answer:
R-C phase shift oscillators use a combination of an amplifier and an RC feedback network to produce output oscillations due to the phase shift between the stages.

R-C phase oscillator is shown below.

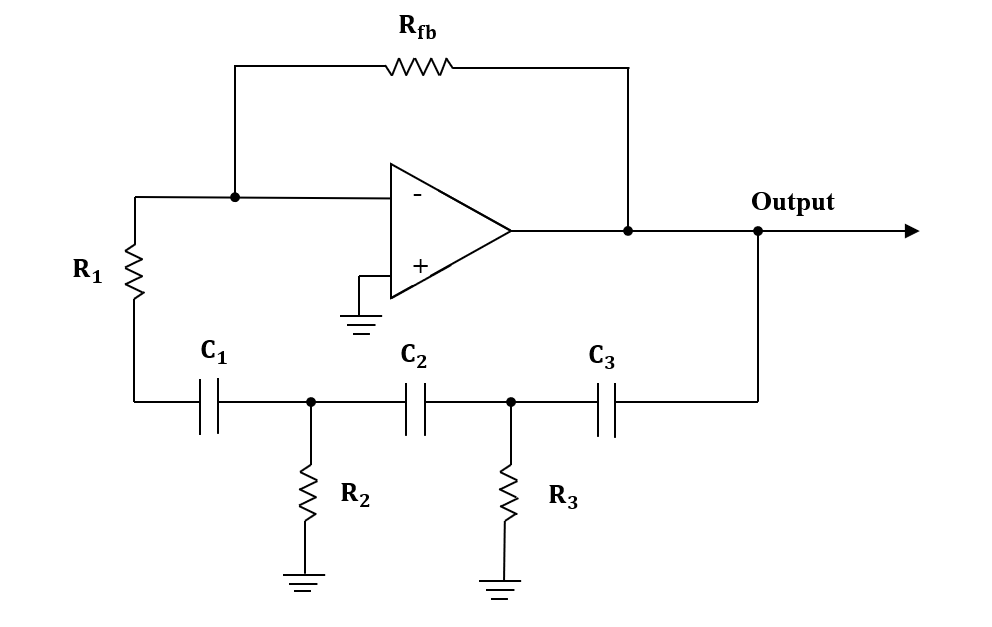
Given: $R= 13k\Omega$
            $C=5 \mu F$
Frequency of a R-C phase-shift oscillator is given by,
$f = \dfrac {1}{2 \pi RC \sqrt {2N}}$ …(1)
Where, R is the feedback resistance
             C is the feedback capacitance
             N is the number of RC combinations
Here, we have three RC combinations. So, N= 3.
Substituting values in the equation. (1) we get,
$f=\dfrac {1} {2 \pi \times 13 \times {10}^{3} \times 5 \times {10}^{-6} \sqrt {6}}$
$\Rightarrow f = \dfrac {1} {1.0004}$
$\Rightarrow f= 0.999$
$\Rightarrow f \approx 1 Hz$
Hence, the frequency of oscillation is 1 Hz.

Note:
If we want to vary the frequency then this can be done by varying one or more of the resistors or the capacitors in the phase-shift network. RC phase shift oscillators are generally used for low frequencies. The output which we get from this RC circuit is sinusoidal in nature. This circuit is not expensive and gives excellent frequency stability. Disadvantage of this circuit is that the output from this circuit is very small because of smaller feedback.