Question

Draw $\angle POQ$ of measure $75{}^\circ $ and find its line of symmetry.

Answer 1

Hint: To draw an angle measures $75{}^\circ $, first we have to draw an angle of $60{}^\circ $ and an angle of $90{}^\circ $ by using the compass. Then, bisect the total angle to get the angle of $75{}^\circ $. To draw a line of symmetry we have to draw a line which bisects the angle $\angle POQ$.

Complete step by step answer:
We have to construct a $\angle POQ$ of measure $75{}^\circ $ and find its line of symmetry.
We know that an angle is drawn between two lines.
So, first let us draw a straight line from a point $O$ and mark the line as $OQ$ which is the base of the angle.

Now, by using the compass let us draw an arc of any radius which intersects the line $OQ$ at a point $A$.

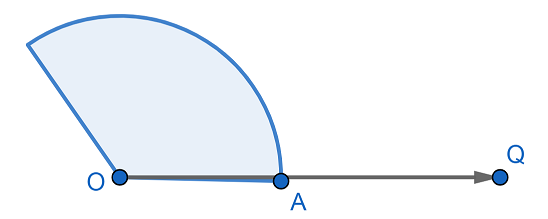
Now, by taking the same radius and point $A$ as center cut the arc drawn previously at point $B$.

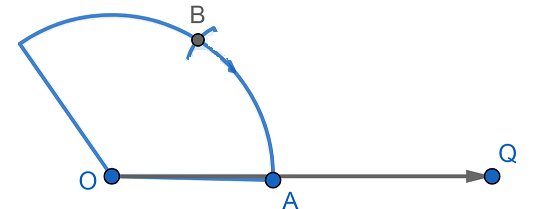
Now, join the line $OB$, the angle $\angle BOA=60{}^\circ $.

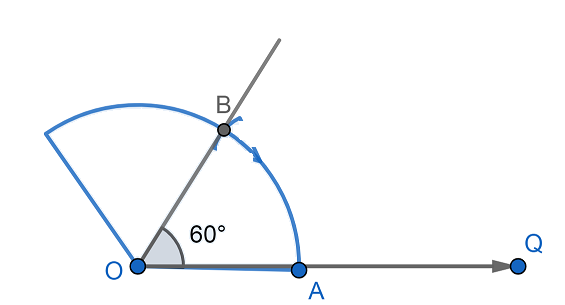
Now, taking the same radius and point $B$ as center cut the arc drawn previously at point $C$.

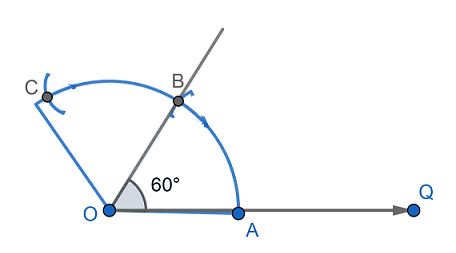
Then, draw the bisector of $\angle BOC$ and mark it as point $D$.
The angle we get is $\angle DOA=90{}^\circ $.

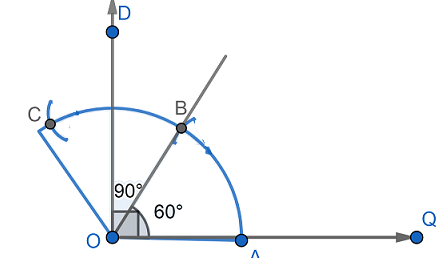
Now, draw an angle bisector of $\angle DOB$ and mark as point $P$.
So, the angle we get is $\angle POQ=75{}^\circ $.

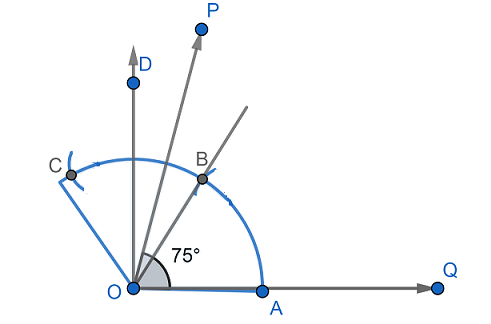
Now, to draw the line symmetry of $\angle POQ$, we draw a line from point $O$ which bisects angle $\angle O$.

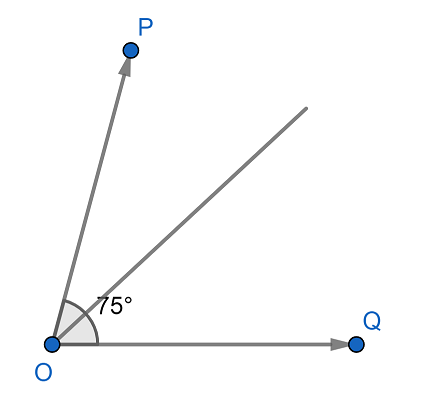
Note: The key concept to construct an angle is to draw an angle bisector. Also, line symmetry is a mirror image taking place across a line.