Question

Draw $\angle ABC$ of measure $120^\circ $ and bisect it.

Answer 1

Hint – As we can see this is the question of geometry, so we will solve it step by step by explaining all the steps and will draw the diagram according to that step and eventually we will get our resultant figure.

Complete step-by-step answer:
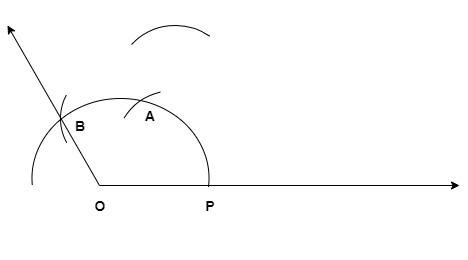
1) Draw a horizontal line (a ray, to be precise) and mark it’s starting point as O.

2) Now take the compass and adjust any suitable angle in it.
3) With the starting point of the ray (i.e. O) as the center, draw a semi-circle, touching the ray.

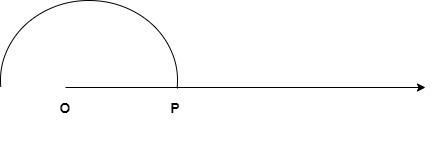
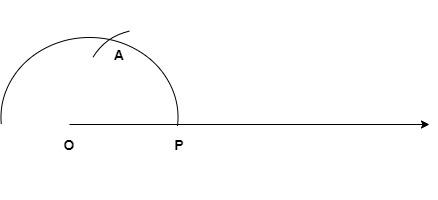
4) Now without changing the angle of the compass, keep it on the point where the semi-circle touches the ray (say P).
5) Draw an arc which intersects the semi-circle at a point (say A).

6) Now keep the compass at A and draw an arc, which intersects the semi-circle at a point (say B).

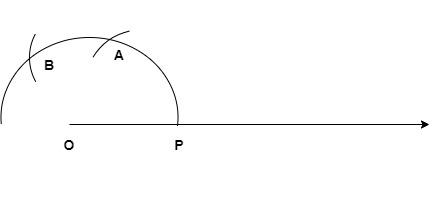
7) Now draw a ray from O to B and extend it. This is $120^\circ $ and by doing this step, we are halfway done.

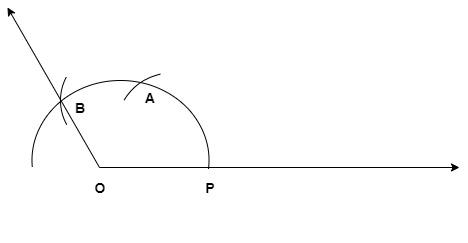
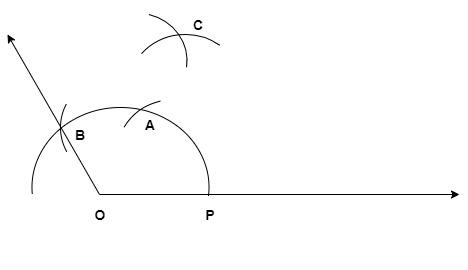
8) Now keep the compass with a definite angle at P and draw an arc inside the angle.

9) Similarly, with B as center (with the same angle in compass), draw an arc which intersects the previously drawn arc at a point (say C).

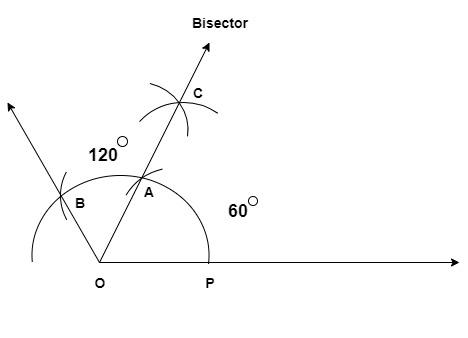
10) Now draw a ray from O to C and extend it. This is the bisector line and by doing this step we will be obliged to hear that we have completed the question and here we get our desired figure.
Where OC is a bisector, $\angle $BOP = 120$^\circ $ and $\angle $AOC = 60$^\circ $

Note – Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A student should follow this approach i.e. Step-By-Step to solve geometry questions as missing or skipping one step will lead to a disastrous result. Thus, we have to follow only this method.