Question

Draw a triangle ABC with BC = 7cm, $\angle \text{B=45}{}^\circ $ and $\angle \text{A=105}{}^\circ $. Then construct another triangle whose sides are $\dfrac{4}{3}$ time the corresponding sides of $\Delta \text{ABC}$. Write the construction.

Answer 1

Draw a triangle ABC with BC = 7cm, $\angle \text{B=45}{}^\circ $ and $\angle \text{A=105}{}^\circ $. Then construct another triangle whose sides are $\dfrac{4}{3}$ time the corresponding sides of $\Delta \text{ABC}$. Write the construction.

Complete step-by-step answer:

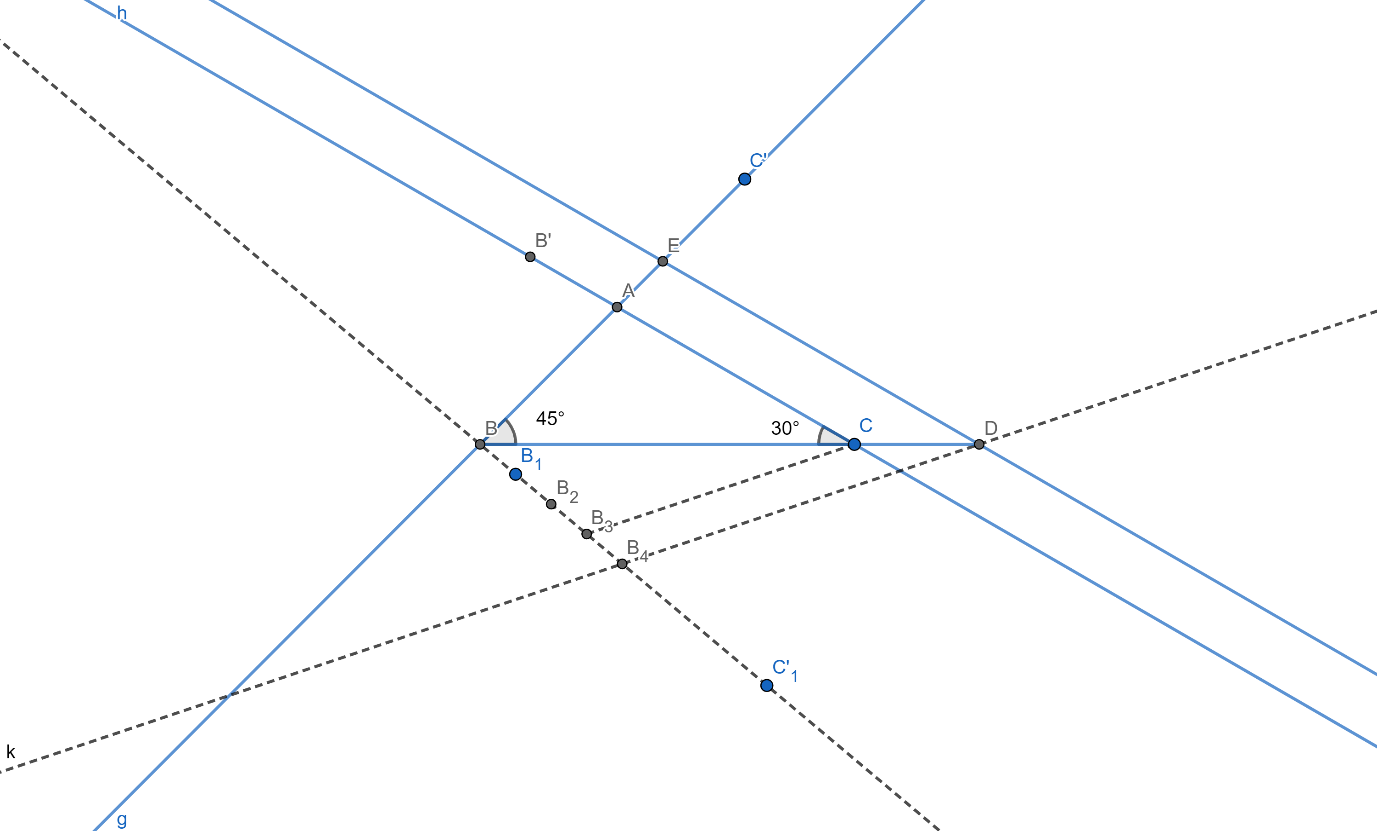
Calculation of measure of angle C:
We have
$\begin{align}
  & \angle \text{A+}\angle \text{B+}\angle \text{C=180}{}^\circ \\
 & \Rightarrow \angle \text{C=180}{}^\circ \text{-150}{}^\circ \text{=30}{}^\circ \\
\end{align}$
$Steps$ $for$ $Construction:$
[1] Draw a line segment BC = 7cm.
[2] Now Draw angle C’BC $=45{}^\circ $ and B’CB $=30{}^\circ $.
[3] Let the line C’B and CB’ intersect at A
[4] ABC is the required triangle.
[5] Now on the opposite side of BC to A draw and acute angle ${{\text{C}}^{'}}_{1}\text{BC}$.
[6] Mark four equidistant point ${{\text{B}}_{1}},{{\text{B}}_{2}},{{\text{B}}_{3}}$ and ${{\text{B}}_{4}}$ such that $\text{B}{{\text{B}}_{1}}={{\text{B}}_{1}}{{\text{B}}_{2}}={{\text{B}}_{2}}{{\text{B}}_{3}}={{\text{B}}_{3}}{{\text{B}}_{4}}$
[7] Join ${{\text{B}}_{3}}$ and C.
[8] Draw a line parallel to ${{\text{B}}_{3}}\text{C}$ and let it intersect BC produced at D.
[9] Draw a line parallel to AC through D and let it intersect AC produced at E
[10] Triangle EBD is the required triangle whose sides are $\dfrac{4}{3}$ times the sides of triangle ABC.

Note: Justification of the construction.
[1] In triangle ABC, we have BC = 7cm, $\angle \text{B=45}{}^\circ $ and $\angle \text{C=30}{}^\circ $, by construction
Hence $\angle \text{A=180}{}^\circ \text{-}\left( 45{}^\circ +30{}^\circ \right)=105{}^\circ $.
Hence we have created a triangle ABC in which BC = 7cm, $\angle \text{B=45}{}^\circ $ and $\angle \text{A=105}{}^\circ $.
Also, by ASA congruence criterion, the triangle ABC is unique.
[2] We begin by showing the triangle ABC and EBD are similar.
Since ED||AC, we have
$\angle \text{A=}\angle \text{E}$ and $\angle \text{C=}\angle \text{D}$.
Also, $\angle \text{B}$ is common to the two triangles.
Hence the triangles are similar by AAA similarity. i.e $\Delta \text{ABC}\sim \Delta \text{EBD}$
Now in the triangle $\text{B}{{\text{B}}_{4}}\text{D}$, we have ${{\text{B}}_{3}}\text{C}\parallel {{\text{B}}_{4}}\text{D}$, hence by basic proportionality theorem, we have
$\dfrac{\text{BC}}{\text{BD}}=\dfrac{\text{B}{{\text{B}}_{3}}}{\text{B}{{\text{B}}_{4}}}=\dfrac{3}{4}$
Now since $\Delta \text{ABC}\sim \Delta \text{EBD}$, we have
$\dfrac{\text{AB}}{\text{EB}}=\dfrac{\text{AC}}{\text{ED}}=\dfrac{\text{BC}}{\text{BD}}=\dfrac{3}{4}$
Hence the sides of triangle EBD are $\dfrac{4}{3}$ times the corresponding sides of ABC.
Hence the construction is justified.