Question

Draw a simple diagram of a hydraulic jack and explain its working.

Answer 1

Hint: This question can be solved by understanding what a hydraulic jack is. It is a device that lifts objects such as a car. The working of a hydraulic jack is based on Pascal’s law, wherein a change in pressure applied to an enclosed liquid transmits it undiminished. In other words, pressure is the same throughout the entire enclosed liquid.

Complete step-by-step solution:
Hydraulic jack works based on a principle known as Pascal’s law. According to Pascal’s law, if a pressure difference is enforced on a fluid enclosed in a chamber, the pressure will be transmitted without any change throughout the fluid and also to the walls of the container. This happens because the atoms in the enclosed fluid are free to move about; hence it is possible for the pressure to reach everywhere.
In this diagram, the container with the large dimension lifts weights whereas the force is applied on the container with the smaller dimension.

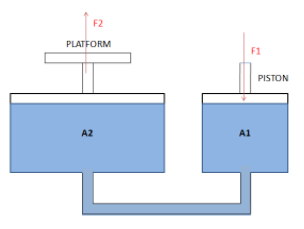
When a force is applied on the container with the smaller dimension, that is the right piston, a change in pressure is developed. This change in pressure is transmitted throughout the fluid without any change in pressure. This causes an upward force (${F_2}$) on the piston on the left-hand side. The force ${F_2}$ is greater than ${F_1}$ because the left piston has a larger surface area compared to the right piston. Therefore the object on the platform gets raised to a higher position.
Mathematically,
According to Pascal’s law \[{P_1}\; = {P_2}\]
Where, P stands for pressure. Pressure is equal to force per unit area.
Therefore $\dfrac{{{F_1}}}{{{A_1}}} = \dfrac{{{F_2}}}{{{A_2}}}$
Rearranging we get, ${F_2} = \dfrac{{{A_2}}}{{{A_1}}}{F_1}$
Since the surface area of ${A_2}$ is greater than the surface area of ${A_1}$, we get the upward force ${F_2}$ is larger than the downward or applied force ${F_1}$.
Therefore the object on the platform is raised because the force acting upward is greater than the applied force.

Note: From the expression that we derived, it can be observed that the force used to lift an object is directly proportional to the ratio of the area of the containers. Another important note is that both the pistons on the right and left sides are at the same height. Therefore there won’t be any pressure due to a change in height or depth value.