Question

Draw a rough sketch and find the area of the region bounded by the parabolas $ {{y}^{2}}=4x\ and\ {{x}^{2}}=4y $ , using the method of integration.

Answer 1

Hint: We will start by drawing the rough sketch of $ {{y}^{2}}=4x\ and\ {{x}^{2}}=4y $ . Then we will find their point of intersection by solving the curve. Then we will use integration to find the area of the bounded region.

Complete step-by-step answer:
Now, we will first draw a rough sketch of $ {{y}^{2}}=4x\ and\ {{x}^{2}}=4y $ as we know that both these equations are of parabola. Therefore, we have,

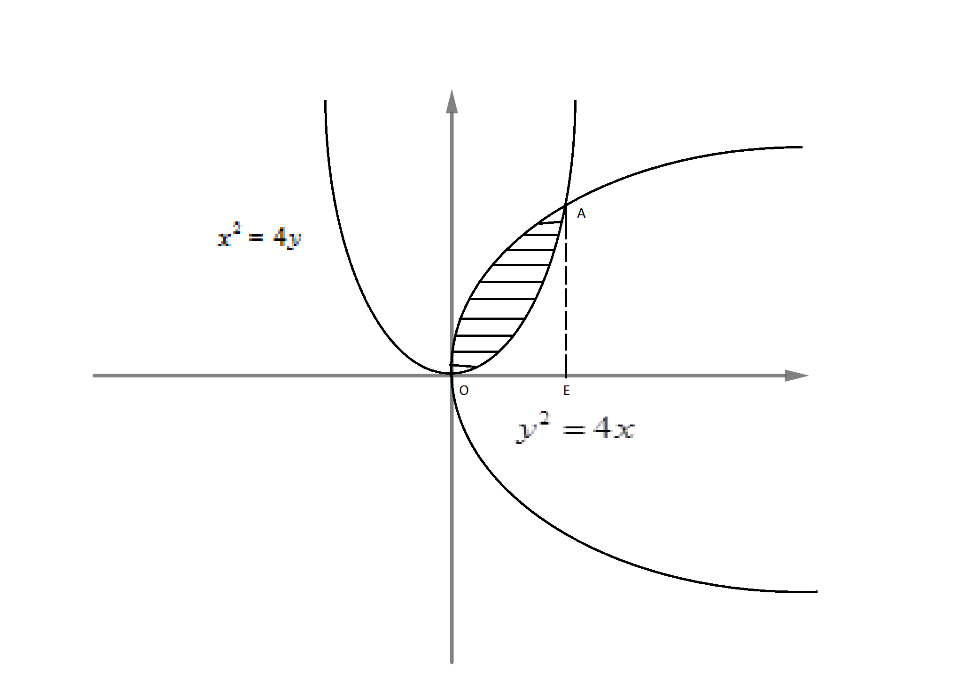
Now, we will first find the point A which is point of intersection of $ {{y}^{2}}=4x $ .
 $ \begin{align}
  & {{y}^{2}}=4x........\left( 1 \right) \\
 & {{x}^{2}}=4y........\left( 2 \right) \\
\end{align} $
Now, we will substitute the value of y from (2) in (1).
\[\begin{align}
  & \Rightarrow {{\left( \dfrac{{{x}^{2}}}{4} \right)}^{2}}=4x \\
 & \Rightarrow \dfrac{{{x}^{4}}}{16}=4x \\
 & \Rightarrow {{x}^{4}}=64x \\
 & \Rightarrow {{x}^{4}}-64x=0 \\
\end{align}\]
Now, by taking x as common we have,
\[\begin{align}
  & x\left( {{x}^{3}}-64 \right)=0 \\
 & \Rightarrow x=0\ or\ x=4 \\
\end{align}\]
Now, substituting x = 0 and x = 4 in (1) we have,
\[\begin{align}
  & \Rightarrow {{y}^{2}}=4\times 0 \\
 & \Rightarrow {{y}^{2}}=0 \\
 & \Rightarrow y=0 \\
 & Also \\
 & \Rightarrow {{y}^{2}}=4\times 4 \\
 & \Rightarrow {{y}^{2}}=16 \\
 & \Rightarrow y=\pm 4 \\
\end{align}\]
Now, since from (2) we have y > 0. Therefore, y = -4 is rejected. Hence, the coordinate of point A is (4, 4).
Now, the area of shaded region is,
ar upper region OAE – ar lower region OA
\[\begin{align}
  & \Rightarrow \int\limits_{0}^{4}{\sqrt{4x}dx}-\int\limits_{0}^{4}{\dfrac{{{x}^{2}}}{4}dx} \\
 & \Rightarrow \int\limits_{0}^{4}{2\sqrt{x}dx}-\int\limits_{0}^{4}{\dfrac{{{x}^{2}}}{4}dx} \\
\end{align}\]
Now, we know that the integral \[\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}}\].
\[\begin{align}
  & \Rightarrow \left( 2\dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right)_{0}^{4}-\left( \dfrac{{{x}^{3}}}{12} \right)_{0}^{4} \\
 & \Rightarrow \dfrac{4}{3}\left( {{x}^{\dfrac{3}{2}}} \right)_{0}^{4}-\dfrac{1}{12}\left( {{x}^{3}} \right)_{0}^{4} \\
 & \Rightarrow \dfrac{4}{3}\left( {{\left( 4 \right)}^{\dfrac{3}{2}}} \right)-\dfrac{1}{12}\left( {{4}^{3}} \right) \\
 & \Rightarrow \dfrac{4}{3}\left( {{2}^{3}} \right)-\dfrac{1}{12}\times {{4}^{3}} \\
 & \Rightarrow \dfrac{32}{3}-\dfrac{16}{3} \\
 & \Rightarrow \dfrac{16}{3}sq\ units \\
\end{align}\]

Note: It is important to note that while solving the question we have taken the limits as x = 0 to x = 4 in both the integral. Also we have subtracted the area formed by the lower region OAE from the upper region to find the bounded area.